5 July 2021 / REINFORCEMENT

Reinforcement Learning - Sales and Advertisement

문제정의

고객에게 가격할인, 회원 딜과 같은 프리미엄 회원제에 가입할 수 있는 옵션을 제공해 할인된 가격, 특가 상품 등과 같은 혜택을 제공한다. 구독할 수 있는 옵션을 제공하는것이 포함되어 있다. 연간 200달러의 가격에 제공되며, 최대한 많은 고객을 프리미엄 회원제에 가입시키는 것이다. 비즈니스 수익을 극대화하기 위해 AI를 구축한다. 1억명의 고객이 있다고 가정하며 프리미엄 회원으로 전환하도록 유도하는 전환율을 가진 전략이 존재한다.

시뮬레이션 내부에 환경 구축하기

고객이 프리미엄 회원제에 가입했다면 보상은 1, 그렇지 않은 경우 보상은 0이다. 이것을 정리하면

1라운드 : 고객 1에게 전략 1의 광고 1을 표시하고 고객이 가입을 결정하는지를 확인한다. 고객이 가입하면 보상으로 1을 받고 그렇지 않으면 봇아으로 0을 받는다. 보상을 수집하면 다음 고객(라운드)으로 넘어간다.

2라운드 : 새로운 고객, 고객 2에게 전략 2의 광로 2를 표시하고 고객이 가입하는지 확인한다. 가이바면 보상으로 1을 받고 그렇지 않으면 보상으로 0을 받는다. 보상을 수집하면 다음 고객으로 넘어간다.

…

10라운드 : 톰슨 샘플링을 통해 어느 광고가 가장 많은 고객을 프리미엄 회원제 가입으로 전환시킬 수 있는 능력이 가장 강한지 알려준다. 우리의 목표는 이 추가 수익을 얻는 데 있다. 톰슨 샘플링으로 결정된 AI는 새로운 고객, 고객 10에게 9가지 광고 중 하나를 선택해 보여주고 가입했는지 확인한다. 가입하면 보상으로 1을 받고 그렇지 않으면 0을 받는다. 보상을 수집하면 다음 고객으로 넘어간다.

…

이 과정을 반복해 AI가 가장 높은 전환율을 보이는 최상의 광고를 찾을 때까지 반복한다.

다음의 전환율을 가정하면

전략	전환율
1	0.05
2	0.13
3	0.09
4	0.16
5	0.11
6	0.04
7	0.20
8	0.08
9	0.01

가장 높은 전환율을 보이는 전략이 7번이라는것을 안다. 하지만 톰슨 샘플링은 이 사실을 모른다. 톰슨 샘플링은 이전 라운드까지 누적된 성공횟수와 실패 횟수만 알고있다.

시뮬레이션 실행

예를들어 전환율이 0.16인 전략은 각 고객에 대해 0과 1사이의 무작위 수를 뽑는다. 이 무작위 수가 0에서 0.16 사이 값일 확률이 16%이며 0.16과 1사이 값일 확률은 84%이다. 따라서 무작위 수가 0과 0.16사이라면 보상으로 1을 얻고, 0.16에서 1사이라면 0을 얻는다. 이것은 회원제에 가입할 확률이 16%인 사실을 나타낸다.

AI Solution

10000번의 라운드에 걸쳐 각 라운드 $n$마다 다음 세 단계를 반복한다.

1단계 : 각 전략 $i$에 대해 다음 분포에서 무작위 값을 뽑는다.

$\theta_{i}(n) \sim \beta(N_{i}^{1}(n) + 1, N_{i}^{0}(n) + 1)$

2단계 : 가장 높은 $\theta_{i}(n)$을 갖는 전략 $s(n)$을 선택한다.

$s(n) = argmax_{i \subseteq \{1,\cdots,9\}}(\theta_{i}(n))$

3단계 : 다음 조건에 따라 $N_{s(n)}^{1}(n)$과 $N_{s(n)}^{0}(n)$을 업데이트한다.

선택된 전략 $s(n)$이 보상으로 1을 받으면 $N_{s(n)}^{1}(n) : = N_{s(n)}^{1}(n) + 1$

선택된 전략 $s(n)$이 보상으로 0을 받으면 $N_{s(n)}^{0}(n) : = N_{s(n)}^{0}(n) + 1$

구현

톰슨 샘플링 대 무작위 선택

톰슨 샘플링을 구현하면서 라운드마다 임의로 전략을 선택하는 무작위 선택 알고리즘도 구현한다. 이 알고리즘은 톰슨 샘플링 모델의 성능을 평가하기 위한 기준이 되며 동일한 환경 행렬에서 경쟁한다.

성능지표 마지막으로 전체 시뮬레이션이 끝나면 다음 공식에 의해 정의된 상대 수익률을 계산해 톰슨샘플링의 성능을 평가할 수 있다.

상대 수익률 = $\frac{(톰슨 샘플링의 보상 총합) - (무작위 선택의 보상 총합)}{무작위 선택의 보상 총합}$

Code

import numpy as np
import matplotlib.pyplot as plt
import random

N = 10000 # 고객 수
d = 9 # 전략 수

conversion_rates = [0.05, 0.13, 0.09, 0.16, 0.11, 0.04, 0.2, 0.08, 0.01]
X = np.array(np.zeros([N, d]))
for i in range(N):
    for j in range(d):
        if np.random.rand() <= conversion_rates[j]:
            X[i, j] = 1

# 라운드마다 무작위 선택 알고리즘에 의해 선택된 전략을 포함한 리스트.
strategies_selected_rs = []

# 라운드마다 톰슨 샘플링 모델에 의해 선택된 전략을 포함한 리스트.
strategies_selected_ts = []

#무작위 선택 알고리즘에 의해 라운드가 반복될 때마다 누적된 보상의 총합
total_reward_rs = 0

#톰슨 샘플링 모델에 의해 라운드가 반복될 때마다 누적된 보상의 총합
total_reward_ts = 0

# 9개의 요소로 이루어진 리스트로 각 전략이 보상으로 1을 받은 횟수를 포함하고 있다.
numbers_of_rewards_1 = [0] * d

# 9개의 요소로 이루어진 리스트로 각 전략이 보상으로 0을 받을 횟수를 포함하고 있다.
numbers_of_rewards_0 = [0] * d

for n in range(0, N):
    # 무작위 선택
    strategy_rs = random.randrange(d)
    strategies_selected_rs.append(strategy_rs)
    reward_rs = X[n, strategy_rs]
    total_reward_rs = total_reward_rs + reward_rs
    
    # 톰슨 샘플링
    strategy_ts = 0
    max_random = 0
    for i in range(0, d):
        random_beta = random.betavariate(numbers_of_rewards_1[i] + 1,
                                        numbers_of_rewards_0[i] + 1)
        
        if random_beta > max_random:
            max_random = random_beta
            strategy_ts = i

    reward_ts = X[n, strategy_ts]
    if reward_ts == 1:
        numbers_of_rewards_1[strategy_ts] = numbers_of_rewards_1[strategy_ts] + 1
    else:
        numbers_of_rewards_0[strategy_ts] = numbers_of_rewards_0[strategy_ts] + 1
            
    strategies_selected_ts.append(strategy_ts)
    total_reward_ts = total_reward_ts + reward_ts

relative_return = abs(total_reward_ts - total_reward_rs) / total_reward_rs * 100
print('relative return: {:.0f} %'.format(relative_return))

relative return: 93 %

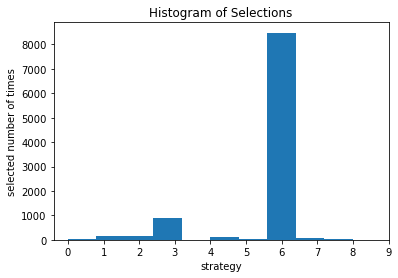
plt.hist(strategies_selected_ts)
plt.title('Histogram of Selections')
plt.xlabel('strategy')
plt.ylabel('selected number of times')
plt.xticks(np.arange(0,10))
plt.show()

참고 : 아들랑 드 폰테베 『강화학습/심층강화학습특강』, 위키북스(2021), p55-71