Q-Learning Basic

Q-Learning은 강화학습 모델이다. 입력(상태)과 출력(행동) 원칙에 따라 작동한다. 상태, 행동, 보상이 사전에 정의된 환경에서 작동하며, 마르코프 결정 프로세스에 의해 모델링된다. 또한 훈련 모드와 추론 모드를 사용하고 훈련 모드 동안 Q-Value라 부르는 매개변수를 학습한다. 또한 상태와 행동의 수는 유한하다.

미로

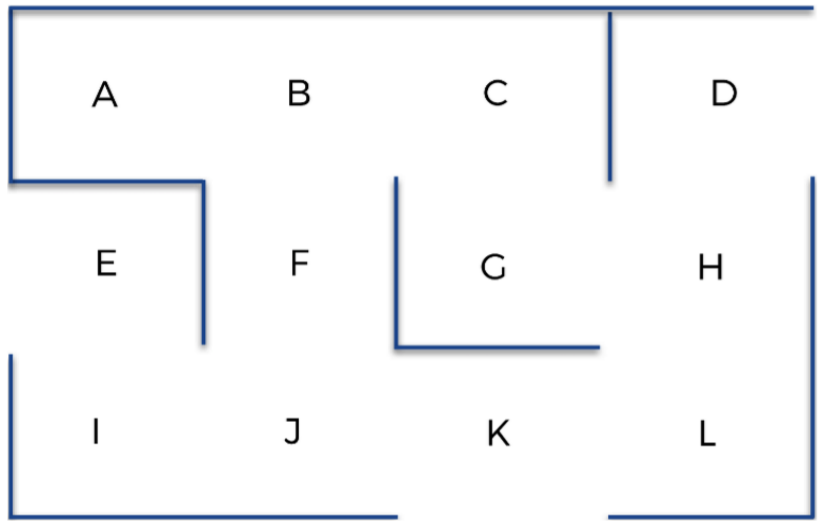
출발점에서 도착점까지 갈 수 있는 AI를 구성해보자. 첫번째로 환경을 구성해야한다.

환경

상태

상태는 AI의 입력이다. 그리고 AI가 최종 목표로 이끌 행동을 취하기 충분한 정보를 담고 있어야 한다. 즉 특정 시간에 AI가 위치한 지점을 나타내는 A부터 L까지의 문자가 될것이다.

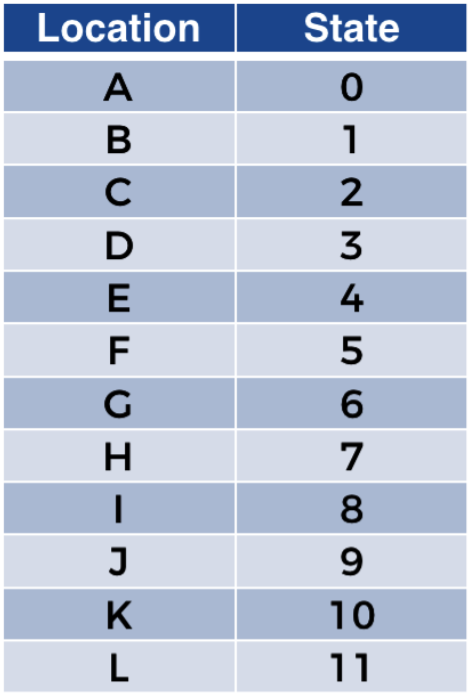
행동

행동은 AI가 한 위치에서 다음 위치로 이동하는 움직임이 될것이다. 예를들어 J에 위치한다면 다음에 수행할 수 있는 행동은 I, F, K로 이동하는것이다. AI가 수행할 수 없는 작업에 보상으로 0을 부여하고 수행 가능한 작업에 보상으로 1을 부여할 수 있다.

보상

구체적으로 상태 $s$와 행동 $a$를 입력으로 취하고 AI가 상태 $s$에서 작업 $a$를 수행해 얻을 수 있는 숫자 보상 $r$을 반환하는 함수 $R$을 정의해야한다.

$R:(s,a) \rightarrow r \subseteq R$

함수에서 $s$는 행렬의 행 인덱스, $a$는 행렬의 열 인덱스, $r$은 이 행열에서 $(s,a)$ 인덱스에 해당하는 행렬을 만든다. A에서는 B로만 이동할 수 있다. 따라서 A의 인덱스는 0이고 B의 인덱스는 1이므로 보상 행렬의 첫번째 행에서는 두번째 열만 1을 갖고 나머지 열은 모두 0을 갖는다. 최종적으로 얻을 보상 행렬은 다음과 같다.

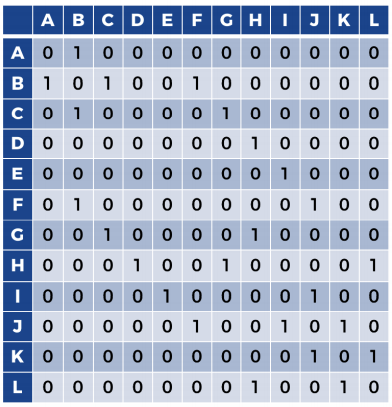
만약 AI가 최우선 위치 G로 이동해야 한다는 것을 어떻게 알릴 수 있을까? G에 높은 보상을 부여하면 다른 위치의 보상보다 훨씬 크기 때문에 AI는 자동으로 높은 보상을 잡으려고 한다. 즉 AI는 항상 최고의 보상을 찾는다. 때문에 G에 도달하는 비결은 다른곳보다 높은 보상을 부여하는것이다. 이에따른 보상행렬은 다음과 같다.

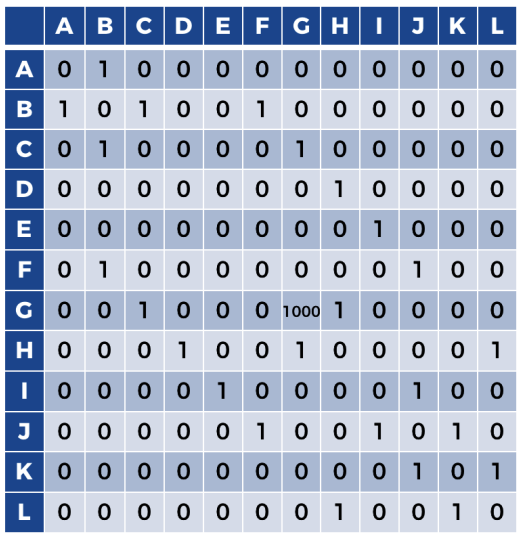
AI 구성

Q-Value

Q-Value는 상태와 행동의 쌍 $(s,a)$마다 숫자 값 $Q(s,a)$와 연결시킨다.

$Q:(s \subseteq S, a \subseteq A) \rightarrow Q(s,a) \subseteq R$

$Q(s,a)$는 상태 $s$에서 행동 $a$를 수행할 때 Q-value 이다.

시간차

특정 시간 $t$에 특정상태 $t_{s}$에 있다고 하자. 선택할 수 있는 행동 중 임의의 행동을 수행하자. 그 결과 다음 상태 $s_{t+1}$로 바뀌고 보상으로 $R(s_{t}, a_{t})$를 얻는다.

시간 $t$에서 시간차를 나타내는 $TD_{t}(s_{t}, a_{t})$는 다음 둘 사이의 차이다.

1. 상태 $s_{t}$에서 행동 $a_{t}$를 수행함으로써 얻는 보상 $R(s_{t},a_{t})$에 미래 상태 $s_{t+1}$에서 수행된 최고 행동의 Q-value에 할인 계수(discount factor) $\gamma \subseteq [0, 1]$에 의해 할인된 값을 더한 값

$R(s_{t},a_{t}) + \gamma max_{a}(Q(s_{t+1},a))$

1. 상태 $s_{t}$에서 행동 $a_{t}$를 수행할 때 Q-value인 $Q(s_{t},a_{t})$

그 결과 다음 식이 도출된다.

$TD_{t}(s_{t}, a_{t}) = R(s_{t}, a_{t}) + \gamma max_{a}(Q(s_{t+1}, a)) - Q(s_{t}, a_{t})$

훈련 초기에 Q-value는 0으로 설정된다.AI는 더 나은 보상을 얻으려고 하기 때문에 시간차가 가장 큰 경우를 찾는다. AI가 받는 보상이 크면 그 큰 보상으로 이어진 (상태, 행동)의 특정 Q-value가 증가하므로 AI는 높은 보상에 도달한 방법을 기억할 수 있다. 상태 $s_{t}$에서 높은 보상 $R(s_{t}, a_{t})$를 받을 수 있는 행동이 $a_{t}$라고 하자. 이는 Q-value $Q(s_{t}, a_{t})$이 자동으로 증가함을 뜻한다. 이렇게 증가한 Q-value는 AI에게 어디로 전이해야 좋은 보상을 받을 수 있는지 알려주기 때문에 중요한 정보가 된다.

AI를 만드는 다음 단계는 나은 보상을 찾는 것뿐 아니라 그와 동시에 높은 Q-value를 찾는 것이다. Q-value가 높으면 훌륭한 보상으로 이어지기 때문이다. 실제로 Q-value가 높으면 더 높은 Q-value로 이어지고 다시 그보다 더 높은 Q-value로 이어져 마지막에는 가장 높은 보상으로 이어진다. 시간차 공식에서 $\gamma max_{a}(Q(s_{t+1},a))$의 역할이다. 어느 시점에서 AI는 좋은 보상과 높은 Q-value로 이어지는 모든 전이를 알게 되며, 이 전이들의 Q-value는 시간이 지남에 따라 이미 증가되었고 결국 시간차는 감소한다. 즉 최종 목표에 가까워질수록 시간차는 작아진다.

결론적으로 시간차는 일시적인 내재적 보상과 같으며 AI는 훈련을 시작할 때 큰 값을 찾으려 한다. 결국 AI는 훈련이 끝날 때 이 보상을 최소화한다.

벨만 방정식

AI가 목표를 달성하도록 이끄는 더 나은 행동을 수행하려면 높은 시간차를 발견했을 때 행동의 Q-value를 증가시켜야 한다. 이러한 Q-value를 업데이트하는 방법은 반복할 때마다 벨만 방정식이라는 다음 방정식을 통해 시간 $t-1$에서 $t$로 Q-value를 업데이트 한다.

$Q_{t}(s_{t},a_{t}) = Q_{t-1}(s_{t},a_{t}) + \alpha TD_{t}(s_{t},a_{t})$

여기에서 $\alpha \subseteq R$은 Q-value의 학습속도를 지정하는 학습률이다. 이 값은 일반적으로 0.75처럼 0과 1사이의 값을 갖는다. $\alpha$값이 작을수로 Q-value의 업데이트는 작아지고 Q-learning이 더 오래 걸린다. $\alpha$값이 클수록 Q-value의 업데이트가 커지고 Q-learning은 빨라진다. 이 방정식에서 알 수 있듯이 시간차 $TD_{t}(s_{t},a_{t})$가 크면 Q-vlaue $Q_{t}(s_{t},a_{t})$가 증가한다.

참고 : 아들랑 드 폰테베 『강화학습/심층강화학습특강』, 위키북스(2021), p72-85