Convolutional Neural Network

완전연결 신경망은 데이터의 형상이 무시된다. 입력 데이터가 이미지인 경우, 이미지는 가로, 세로, 채널로 구성된 3차원 데이터이다. 그러나 오나전연결 계층에 입력할 때는 3차원 데이터를 평평한 1차원 데이터로 평탄화 해줘야한다. 이미지는 3차원 형상이며, 공간적으로 가까운 픽셀은 값이 비슷하거나, RGB채널은 서로 밀접하게 관련되어 있거나, 거리가 먼 픽셀끼리는 관련이 없는 등, 3차원 속에서 형상을 통한 패턴이 숨어있다. 하지만 완전연결 계층은 형상을 무시하고 모든 입력 데이터를 동등한 뉴런으로 취급하여 형상에 담긴 정보를 살릴 수 없다.

하지만 합성곱 계층은 형상을 유지한다. 3차원 데이터로 입력받으며, 다음 계층에도 3차원 데이터로 전달한다. 따라서 CNN은 이미지처럼 형상을 가진 데이터를 제대로 이해할 가능성이 높다.

CNN에서는 합성곱 계층의 입출력 데이터를 feature map이라고 한다. 합성곱 계층의 입력 데이터를 input feature map, 출력 데이터를 output feature map이라고 한다.

합성곱 연산

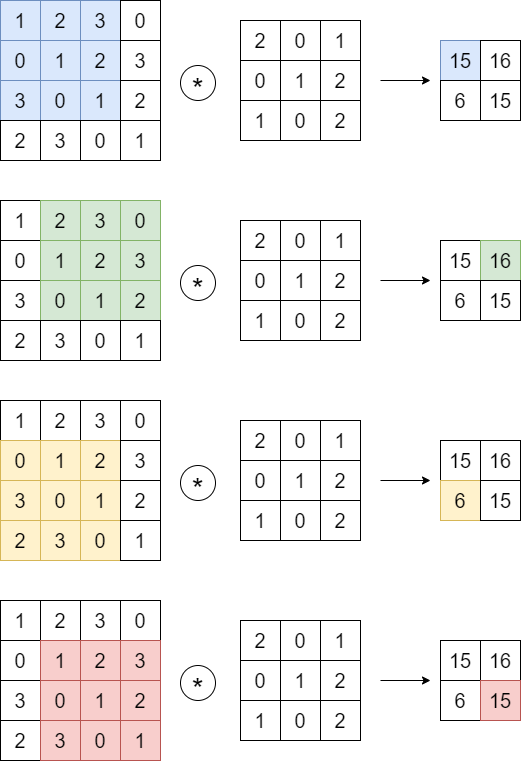
합성곱 연산은 입력 데이터에 필터를 적용한다. 합성곱 연산은 필터의 window를 일정 간격으로 이동해가며 입력 데이터에 적용한다. 입력과 필터에서 대응하는 원소끼리 곱한 후 그 총합을 구한다. 이 과정을 모든 장소에서 수행하면 합성곱 연산의 출력이 완성되며 편향을 적용하면 출력 데이터가 완성된다.

Padding

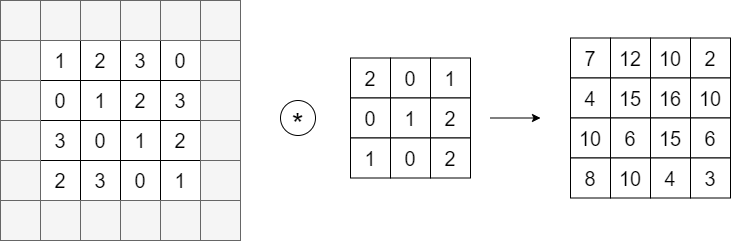
합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정 값으로 채워준다. 이를 padding이라고 하며, 합성곱 연산에서 주로 사용한다. 패딩은 주로 출력 크기를 조정할 목적으로 사용되는데, 합성곱 연산을 거칠 때마다 크기가 작아지면 어느 시점에서는 출력의 크기가 1이 되버린다. 이 문제를 해결하기 위해 패딩을 사용하며, 폭을 1로 설정한 패딩은 입력에 대한 출력이 같은 크기로 유지되게 한다.

Stride

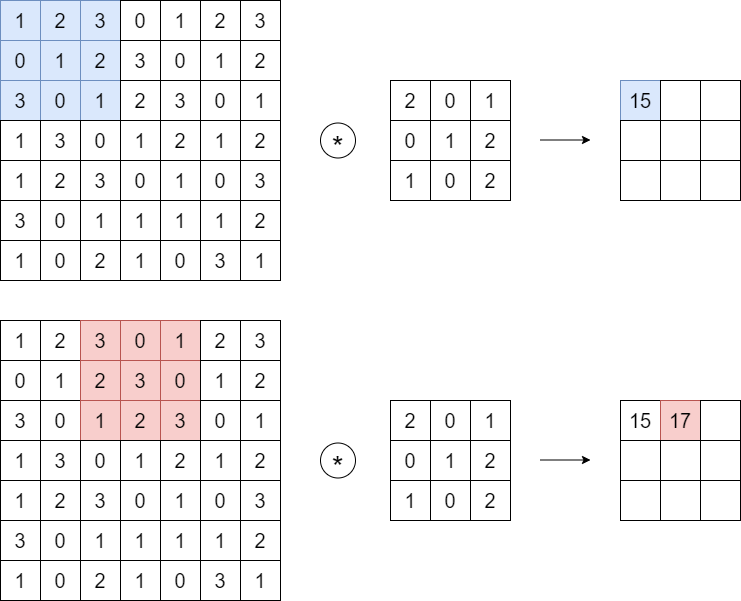
필터를 적용하는 위치의 간격을 Stride라고 한다. Stride를 2로 하면 필터를 적용하는 윈도우가 두칸씩 이동한다.

입력 크기를 (H, W), 필터 크기를 (FH, FW), 출력 크기를 (OH, OW), 패딩을 P, 스트라이드를 S라 하면, 출력의 크기를 다음과 같이 나타낼 수 있다. $OH = \frac{H + 2P - FH}{S} + 1$, $OW = \frac{W + 2P - FW}{s} + 1$

3차원 데이터 합성곱 연산

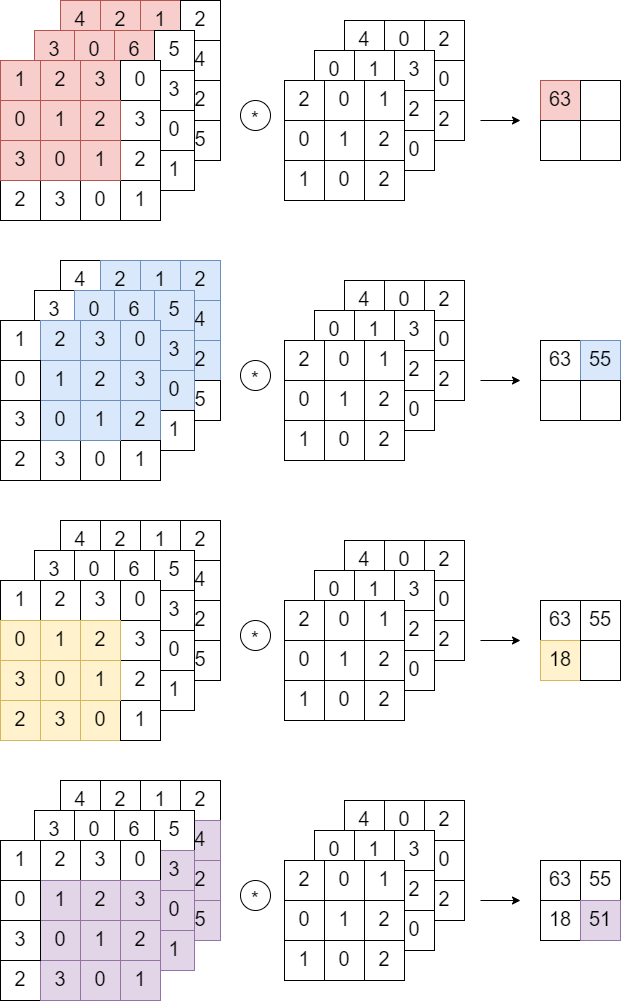
3차원 합성곱 연산에서 주의할 점은 입력 데이터의 채널 수와 필터의 채널 수가 같아야 한다는 것이다.

Pooling 계층

Pooling은 세로, 가로 방향의 공간을 줄이는 연산이다. Max Pooling을 Stride 2로 처리하는 순서를 나타낸다. Max Pooling은 최대값을 구하는 연산으로 2X2 영역에서 가장 큰 원소를 선택한다.

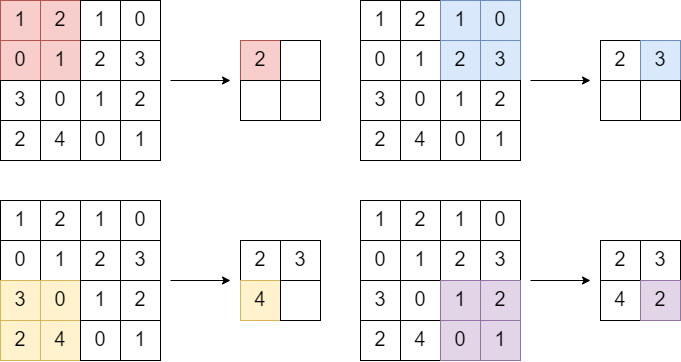
Pooling 계층의 특징으로는

1. 학습해야 할 매개변수가 없다.
   • 풀링 계층은 합성곱 계층과 달리 학습해야 할 매개변수가 없다. 풀리은 대상 영역에서 최댓값이나 평균을 취하는 명확한 처리이므로 학습할 것이 없다.
2. 채널 수가 변하지 않는다.
   • 풀링 연산은 입력 데이터의 채널 수 그대로 출력 데이터로 내보낸다.
3. 입력의 변화에 영향을 적게 받는다.
   • 입력 데이터가 조금 변해도 풀링의 결과는 잘 변하지 않는다.

참고 : 사이토 고키, 『DeepLearning from Scratch』, 한빛미디어(2020), p189-241