Deep Learning from Scratch - Training Skills(3)
Training Issue
기계학습에서는 Overfitting이 문제가 된다. 신경망이 훈련 데이터에만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말한다. 기계학습은 범용적 성능을 지향하고, 새로운 데이터가 주어져도 바르게 식별해내는 모델이 바람직하다.
Overfitting
Overfitting은 주로 다음의 두 경우에 일어난다.
- 매개변수가 많고 표현력이 높은 모델
- 훈련 데이터가 적음
일부러 Overfitting을 일으키기 위해, 300개의 MNIST의 데이터만 사용하고, layer를 7개를 사용해 모델의 복잡성을 높혔다.
from dataset import *
from multi_layer_net import *
from optimizer import *
import matplotlib.pyplot as plt
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
x_train = x_train[:300]
t_train = t_train[:300]
network = MultiLayerNet(input_size = 784, hidden_size_list = [100, 100, 100, 100, 100, 100], output_size=10)
optimizer = SGD(lr = 0.01)
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
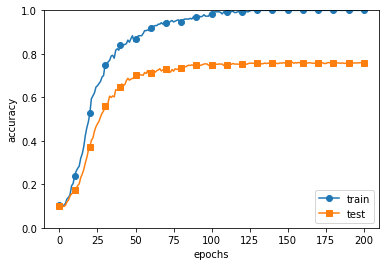
train accuracy와 test accuracy를 그려보면, train에 대해서는 100%의 정확도를 보이지만, test 데이터에 대해서는 큰 차이를 보인다. 정확도가 크게 벌어지는 것은 훈련 데이터에만 적응(fitting)해버린 결과이다.
가중치 감소
Overfitting의 억제용으로 가중치 감소(weight decay)라는 것이 있다. 학습 과정에서 큰 가중치에 대해서는 그에 상응하는 큰 페널티를 부과하여 오버피팅을 억제하는 방법이다. Overfitting은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문이다. 가중치 감소를 이용하면 사용하지 않았을때보다 오버피팅이 약간 억제된다. 또한 훈련 데이터에 대한 정확도가 100%에 도달하지 못한 점도 특징으로 볼 수 있다.
Dropout
신경망 모델이 복잡해지면 가중치 감소만으로는 대응하기 어렵다. 이때 Dropout 기법을 사용한다. Dropout은 뉴런을 임의로 삭제하면서 학습하는 방법이다. 훈련 때 은닉층의 뉴런을 무작위로 골라 삭제한다. 삭제도니 뉴런은 신호를 전달하지 않게 된다. 훈련 때는 데이터를 흘릴 때마다 삭제할 뉴런을 무작위로 선택하고, 시험 때는 모든 뉴런에 신호를 전달한다. 단, 시험 때는 각 뉴런의 출력에 훈련 때 삭제 하지 않은 비율을 곱하여 출력한다.
class Dropout:
def __init__(self, dropout_ratio = 0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg = True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
여기에서 핵심은 훈련 시에는 순전파 때마다 self.mask에 삭제할 뉴런을 False로 표시한다. self.mask는 x와 형상이 같은 배열을 무작위로 생성하고, 그 값이 dropuout_ratio보다 큰 원ㅅ만 True로 설정한다.
import numpy as np
import matplotlib.pyplot as plt
from dataset import load_mnist
from multi_layer_net_extend import MultiLayerNetExtend
from trainer import Trainer
from util import *
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
x_train = x_train[:300]
t_train = t_train[:300]
use_dropout = True
dropout_ratio = 0.2
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=301, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()
train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
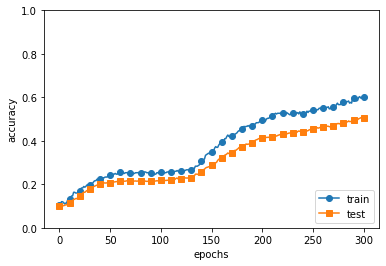
훈련 데이터와 시험 데이터에 대한 정확도 차이가 줄어들었다. 이처럼 Dropout을 이용하면 표현력을 높이면서도 Overfitting을 억제할 수 있다.
Hyperparameter Optimization
Validation Data
하이퍼파라미터의 성능을 평가할 때는 시험 데이터를 사용하는게 아니라 검증 데이터를 사용해야한다. 시험 데이터를 사용하여 하이퍼파라미터를 조정하면 하이퍼파라미터 값이 시험 데이터에 오버피팅되기 때문이다.
(x_train, t_train), (x_test, t_test) = load_mnist()
x_train, t_train = shuffle_dataset(x_train, t_train)
valid_rate = 0.2
valid_num = int(x_train.shape[0] * valid_rate)
x_val = x_train[:valid_num]
t_val = t_train[:valid_num]
x_train = x_train[valid_num:]
t_train = t_train[valid_num:]
Hyperparameter Optimization
Hyperparameter를 최적화할 때의 핵심은 최적 값이 존재하는 범위를 조금씩 줄여간다는 것이다. 대략전인 범위를 설정하고 그 범위에서 무작위로 하이퍼파라미터 값을 골라낸 후, 그 값으로 정확도를 평가한다. 이 작업을 반복하며 하이퍼파라미터의 ‘최적 값’의 범위를 좁혀가는 것이다.
- 0단계 : 하이퍼파라미터 값의 범위를 설정한다.
- 1단계 : 설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출한다.
- 2단계 : 1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고, 검증 데이터로 정확도를 평가한다.(단 Epoch은 작게 설정한다.)
- 3단계 : 1단계와 2단계를 특정 횟수 반복하며, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.
import numpy as np
import matplotlib.pyplot as plt
from dataset import load_mnist
from multi_layer_net import MultiLayerNet
from util import shuffle_dataset
from trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
x_train = x_train[:500]
t_train = t_train[:500]
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
val_acc_list, train_acc_list = __train(lr, weight_decay)
# print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
plt.figure(figsize=(20,10))
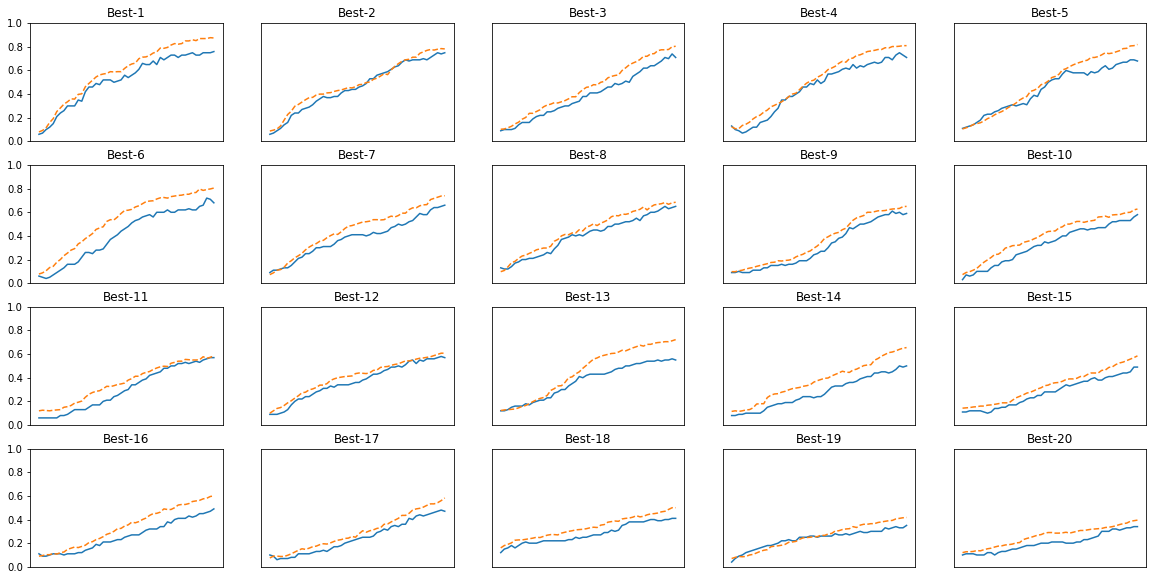
for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i+1)
plt.title("Best-" + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()
Best-1(val acc:0.76) | lr:0.009601940514191675, weight decay:1.0892230161099816e-05
Best-2(val acc:0.75) | lr:0.0055225643305436, weight decay:1.0889727582549518e-06
Best-3(val acc:0.71) | lr:0.008794253771386203, weight decay:4.004334410371384e-08
Best-4(val acc:0.71) | lr:0.004964331678021322, weight decay:9.590524370091789e-08
Best-5(val acc:0.68) | lr:0.005984267879874304, weight decay:1.9616042252157875e-06
Best-6(val acc:0.68) | lr:0.005871582829729415, weight decay:3.57872501821882e-08
Best-7(val acc:0.66) | lr:0.004223656145082359, weight decay:6.545765694062896e-06
Best-8(val acc:0.65) | lr:0.005433844951955731, weight decay:8.297794299721034e-07
Best-9(val acc:0.59) | lr:0.005437540976439739, weight decay:2.9808908725909925e-08
Best-10(val acc:0.58) | lr:0.003597576701410404, weight decay:4.237937758030534e-06
Best-11(val acc:0.57) | lr:0.003439601691219743, weight decay:1.8795025926169585e-06
Best-12(val acc:0.57) | lr:0.0032306911998342003, weight decay:3.8382690872639324e-06
Best-13(val acc:0.55) | lr:0.004384025671042093, weight decay:3.743701917600445e-05
Best-14(val acc:0.5) | lr:0.003953522979911999, weight decay:1.2141984176589071e-05
Best-15(val acc:0.49) | lr:0.0036290726745014583, weight decay:2.237647472108435e-06
Best-16(val acc:0.49) | lr:0.004108118407288531, weight decay:4.3646445107799726e-07
Best-17(val acc:0.47) | lr:0.00401939627276177, weight decay:4.551717159616238e-05
Best-18(val acc:0.41) | lr:0.002891143175247755, weight decay:2.9562931736436558e-06
Best-19(val acc:0.35) | lr:0.002439221646167253, weight decay:1.0060022490906464e-07
Best-20(val acc:0.34) | lr:0.0020447818776639115, weight decay:1.584254866090977e-08
참고 : 사이토 고키, 『DeepLearning from Scratch』, 한빛미디어(2020), p215-226