26 July 2021 / PYTORCH

Pytorch - Logistic Regression

Logistic Regression

Binary Classification

Score에 따른 Pass/Fail 여부를 판정하는 모델을 만든다고 가정할 때, 그래프로 데이터를 표현해보면 S자 형태로 표현된다. 이때 $x$와 $y$의 관계를 $y = Wx + b$가 아닌 특정함수 $f$를 사용하여 $y = f(Wx+b)$를 사용한다.

import numpy as np
import matplotlib.pyplot as plt

score = [45, 50, 55, 60, 65, 70]
result = ['fail','fail','fail','pass','pass','pass']

binary = []
for b in result:
    if b == 'fail':
        binary.append(0)
    else:
        binary.append(1)

plt.plot(score, binary);

png

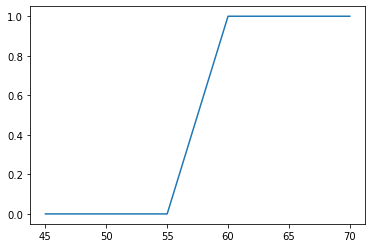
Sigmoid Function

위와 같이 s자 형태의 그래프를 나타낼 수 있는 시그모이드 함수는 다음과 같다.
$y = sigmoid(Wx+b) = \frac{1}{1+e^{-(Wx+b)}} = \sigma (Wx+b)$

def sigmoid(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5, 5, 0.1)
y = sigmoid(x)

plt.plot(x, y);

png

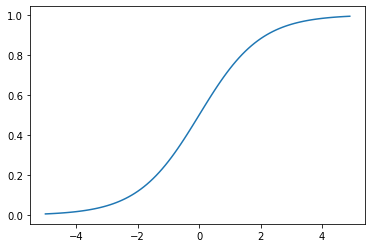
Sigmoid 함수는 입력값이 커질수록 1에 수렴하고, 작아질수록 0에 수렴한다. 출력값은 0과 1사이의 값을 갖는데, 이 특성을 이용해 분류에 사용할 수 있다.

Pytorch

import torch
import torch.nn as nn
import torch.nn.functional as F

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

x_train.shape, y_train.shape

(torch.Size([6, 2]), torch.Size([6, 1]))

W = torch.zeros((2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

y_hat = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))

# or

y_hat = torch.sigmoid(x_train.matmul(W)+b)

$Loss(W) = -\frac{1}{n} \sum_{i=1}^{n} [y^{(i)}logH(x^{(i)}) + (1-y^{(i)})log(1-H(x^{(i)}))]$

print(y_hat)
print(y)

tensor([[0.5000],
        [0.5000],
        [0.5000],
        [0.5000],
        [0.5000],
        [0.5000]], grad_fn=<SigmoidBackward>)
[[0], [0], [0], [1], [1], [1]]

losses = -(y_train * torch.log(y_hat) + (1 - y_train) * torch.log(1 - y_hat))
loss = losses.mean()
print(loss)

# or

loss = F.binary_cross_entropy(y_hat.reshape([6,1]), y_train)
print(loss)

tensor(0.6931, grad_fn=<MeanBackward0>)
tensor(0.6931, grad_fn=<BinaryCrossEntropyBackward>)

Summary

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

optimizer = torch.optim.SGD([W, b], lr=1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    hypothesis = torch.sigmoid(x_train.matmul(W) + b)
    loss = -(y_train * torch.log(hypothesis) + 
             (1 - y_train) * torch.log(1 - hypothesis)).mean()

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Loss: {:.6f}'.format(
            epoch, nb_epochs, loss.item()
        ))

Epoch    0/1000 Loss: 0.693147
Epoch  100/1000 Loss: 0.134722
Epoch  200/1000 Loss: 0.080643
Epoch  300/1000 Loss: 0.057900
Epoch  400/1000 Loss: 0.045300
Epoch  500/1000 Loss: 0.037261
Epoch  600/1000 Loss: 0.031673
Epoch  700/1000 Loss: 0.027556
Epoch  800/1000 Loss: 0.024394
Epoch  900/1000 Loss: 0.021888
Epoch 1000/1000 Loss: 0.019852

Binary Classification with Pytorch Module

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

model = nn.Sequential(nn.Linear(2,1),
                     nn.Sigmoid())

model

Sequential(
  (0): Linear(in_features=2, out_features=1, bias=True)
  (1): Sigmoid()
)

model(x_train)

tensor([[0.6215],
        [0.7648],
        [0.6448],
        [0.8457],
        [0.8768],
        [0.8584]], grad_fn=<SigmoidBackward>)

optimizer = torch.optim.SGD(model.parameters(), lr=1)
epochs = 1000

for epoch in range(epochs+1):
    y_hat = model(x_train)
    loss = F.binary_cross_entropy(y_hat, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch % 100 == 0:
        prediction = hypothesis >= torch.FloatTensor([0.5]) # Threshold = 0.6
        correct_prediction = prediction.float() == y_train
        accuracy = correct_prediction.sum().item() / len(correct_prediction) # Accuracy
        print('Epoch {:4d}/{} Loss: {:.6f} Accuracy {:2.2f}%'.format(epoch, nb_epochs, loss.item(), accuracy * 100,
        ))

Epoch    0/1000 Loss: 0.650903 Accuracy 100.00%
Epoch  100/1000 Loss: 0.128045 Accuracy 100.00%
Epoch  200/1000 Loss: 0.078261 Accuracy 100.00%
Epoch  300/1000 Loss: 0.056682 Accuracy 100.00%
Epoch  400/1000 Loss: 0.044559 Accuracy 100.00%
Epoch  500/1000 Loss: 0.036761 Accuracy 100.00%
Epoch  600/1000 Loss: 0.031313 Accuracy 100.00%
Epoch  700/1000 Loss: 0.027284 Accuracy 100.00%
Epoch  800/1000 Loss: 0.024181 Accuracy 100.00%
Epoch  900/1000 Loss: 0.021717 Accuracy 100.00%
Epoch 1000/1000 Loss: 0.019711 Accuracy 100.00%

Binary Classification with Class

x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

class binary_classification(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(2,1)
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, x):
        return self.sigmoid(self.linear(x))

model = binary_classification()
optimizer = torch.optim.SGD(model.parameters(), lr=1)

for epoch in range(epochs+1):
    y_hat = model(x_train)
    loss = F.binary_cross_entropy(y_hat, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch % 100 == 0:
        prediction = hypothesis >= torch.FloatTensor([0.5]) # Threshold = 0.6
        correct_prediction = prediction.float() == y_train
        accuracy = correct_prediction.sum().item() / len(correct_prediction) # Accuracy
        print('Epoch {:4d}/{} Loss: {:.6f} Accuracy {:2.2f}%'.format(epoch, nb_epochs, loss.item(), accuracy * 100,
        ))

Epoch    0/1000 Loss: 0.869798 Accuracy 100.00%
Epoch  100/1000 Loss: 0.137148 Accuracy 100.00%
Epoch  200/1000 Loss: 0.081484 Accuracy 100.00%
Epoch  300/1000 Loss: 0.058325 Accuracy 100.00%
Epoch  400/1000 Loss: 0.045556 Accuracy 100.00%
Epoch  500/1000 Loss: 0.037433 Accuracy 100.00%
Epoch  600/1000 Loss: 0.031796 Accuracy 100.00%
Epoch  700/1000 Loss: 0.027649 Accuracy 100.00%
Epoch  800/1000 Loss: 0.024467 Accuracy 100.00%
Epoch  900/1000 Loss: 0.021947 Accuracy 100.00%
Epoch 1000/1000 Loss: 0.019900 Accuracy 100.00%