Deep Learning from Scratch - Neural Network Training
Neural Network Training
Loss Function
손실함수는 신경망의 성능의 나쁨을 나타내는 지표로, 현재의 신경망이 훈련 데이터를 얼마나 잘 처리하지 못하느냐를 나타낸다.
신경망 학습에서 최적의 매개변수(w, b)를 탐색할 때 손실 함수의 값을 가능한 한 작게하는 매개변수 값을 찾는다. 이때 매개변수의 미분(gradient)을 계산하고, 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복한다.
SSE
$E = \frac{1}{2} \sum_{k} (y_{k} - t_{k})^{2}$ 여기서 $y_{k}$는 신경망의 출력(예측한 값), $t_{k}$는 정답 레이블, $k$는 데이터의 차원 수를 나타낸다.
import numpy as np
import matplotlib.pyplot as plt
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y_1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
sum_squares_error(np.array(y_1), np.array(t))
0.09750000000000003
y_2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
sum_squares_error(np.array(y_2), np.array(t))
0.5975
CEE
$ E = -\sum_{k}t_{k}logy_{k}$
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
delta를 더하는 이유 : np.log에 0을 입력하면 -inf가 되어 계산을 진행할 수가 없다. 아주 작은 delta값을 더해서 -inf가 발생하지 않도록 구성
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y_1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cross_entropy_error(np.array(y_1), np.array(t))
0.510825457099338
y_2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cross_entropy_error(np.array(y_2), np.array(t))
2.302584092994546
수치 미분
$ y = 0.01x^{2} + 0.1x$
def function_1(x):
return 0.01*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x1b682620748>]
편미분
$f(x_{0}, x_{1}) = x_{0}^{2} + x_{1}^{2}$
def function_2(x):
return x[0]**2 + x[1]**2 # or np.sum(x**2)
기울기
$(\frac{\partial f}{\partial x_{0}}, \frac{\partial f}{\partial x_{1}})$ 처럼 모든 변수의 편미분을 벡터로 정리한것을 기울기라고 한다.
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
it.iternext()
return grad
numerical_gradient(function_2, np.array([3.0, 4.0]))
array([6., 8.])
numerical_gradient(function_2, np.array([0.0, 2.0]))
array([0., 4.])
경사하강법
최적의 매개변수를 찾을 때 최적이란 손실 함수가 최솟값이 될 때의 매개변수 값이다. 기울어진 방향이 꼭 최솟값을 가리키는 것은 아니지만, 그 방향으로 가야 함수의 값을 줄일 수 있다. 그래서 기울기 정보를 단서로 나아갈 방향을 정해야 한다.
$x_{0} = x_{0} - \eta \frac{\partial f}{\partial x_{0}}$
$x_{1} = x_{1} - \eta \frac{\partial f}{\partial x_{1}}$
$\eta$는 갱신하는 양을 나타낸다. 이를 학습률이라고 한다. 한번의 학습으로 얼마만큼 학습해야할지, 매개변수 값을 얼마나 갱신해야할지를 정한다.
def gradient_descent(f, init_x, lr = 0.01, step_num = 100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x = init_x, lr=0.1, step_num = 100)
array([-6.11110793e-10, 8.14814391e-10])
신경망에서의 기울기
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y+delta))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
net = simpleNet()
print(net.W)
[[ 1.48560966 -0.14753772 -0.31133111]
[ 0.84614063 -1.36949181 -0.52690748]]
x = np.array([0.6, 0.9])
p = net.predict(x)
print(p)
[ 1.65289237 -1.32106526 -0.6610154 ]
np.argmax(p)
0
t = np.array([0, 0, 1])
net.loss(x, t)
2.453646622845499
def f(W):
return net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
[[ 0.52174996 0.02666177 -0.54841173]
[ 0.78262494 0.03999266 -0.8226176 ]]
2-Layer Neural Network
from functions import *
from gradient import numerical_gradient
class twolayernet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
acc = np.sum(y == t) / float(x.shape[0])
return acc
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
net = twolayernet(input_size = 784, hidden_size = 100, output_size=10)
x = np.random.rand(100, 784)
y = net.predict(x)
x = np.random.rand(100, 784)
t = np.random.rand(100, 10)
grads = net.numerical_gradient(x, t)
Mini-Batch Training
import tensorflow as tf
from tensorflow.keras.utils import to_categorical
def get_data():
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(-1, 784)
x_test = x_test.reshape(-1, 784)
return x_train, y_train, x_test, y_test
x_train, y_train, x_test, y_test = get_data()
y_train_cat = to_categorical(y_train)
y_test_cat = to_categorical(y_test)
train_loss_list = []
epochs = 1000
train_size = x_train.shape[0]
batch_size = 100
lr = 0.1
network = twolayernet(input_size=784, hidden_size=50, output_size=10)
for epoch in range(epochs):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
y_batch = y_train_cat[batch_mask]
grad = network.numerical_gradient(x_batch, y_batch)
for key in ('W1','b1','W2','b2'):
network.params[key] -= lr * grad[key]
loss = network.loss(x_batch, y_batch)
train_loss_list.append(loss)
if epoch % 100 == 0:
print('Epoch {:4d}/{}, Loss : {:6f}'.format(epoch, epochs, loss.item()))
Summary
import numpy as np
from dataset import load_mnist
(x_train, y_train), (x_test, y_test) = load_mnist(normalize=True, one_hot_label=True)
Downloading train-images-idx3-ubyte.gz ...
Done
Downloading train-labels-idx1-ubyte.gz ...
Done
Downloading t10k-images-idx3-ubyte.gz ...
Done
Downloading t10k-labels-idx1-ubyte.gz ...
Done
Converting train-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting train-labels-idx1-ubyte.gz to NumPy Array ...
Done
Converting t10k-images-idx3-ubyte.gz to NumPy Array ...
Done
Converting t10k-labels-idx1-ubyte.gz to NumPy Array ...
Done
Creating pickle file ...
Done!
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grads['W1'] = np.dot(x.T, da1)
grads['b1'] = np.sum(da1, axis=0)
return grads
network = TwoLayerNet(input_size = 784, hidden_size=50, output_size=10)
epochs = 10000
train_size = x_train.shape[0]
batch_size = 100
lr = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for epoch in range(epochs+1):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
y_batch = y_train[batch_mask]
grad = network.gradient(x_batch, y_batch)
for key in ('W1', 'b1','W2','b2'):
network.params[key] -= lr * grad[key]
loss = network.loss(x_batch, y_batch)
train_loss_list.append(loss)
if epoch % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, y_train)
test_acc = network.accuracy(x_test, y_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print('train acc : {:6f}, test acc : {:6f}'.format(train_acc, test_acc))
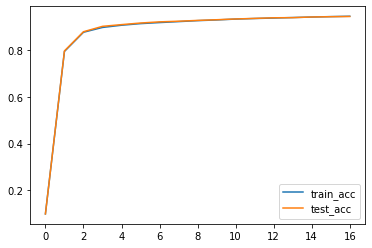
train acc : 0.097517, test acc : 0.097400
train acc : 0.795900, test acc : 0.798200
train acc : 0.878350, test acc : 0.880600
train acc : 0.899017, test acc : 0.903800
train acc : 0.908567, test acc : 0.911200
train acc : 0.915467, test acc : 0.918100
train acc : 0.920017, test acc : 0.923100
train acc : 0.924117, test acc : 0.925800
train acc : 0.928300, test acc : 0.929300
train acc : 0.931283, test acc : 0.932200
train acc : 0.935033, test acc : 0.935500
train acc : 0.937483, test acc : 0.937900
train acc : 0.939500, test acc : 0.940600
train acc : 0.941650, test acc : 0.941200
train acc : 0.943783, test acc : 0.944000
train acc : 0.945633, test acc : 0.945300
train acc : 0.947217, test acc : 0.946200
plt.plot(train_acc_list, label = 'train_acc')
plt.plot(test_acc_list, label = 'test_acc')
plt.legend()
plt.show()
참고 : 사이토 고키, 『DeepLearning from Scratch』, 한빛미디어(2020), p107-146