Deep Learning from Scratch - Training Skills(2)
Weight Initialization
초깃값을 0으로 하면?
가중치 감소는 간단히 말하자면 가중치 매개변수의 값이 작아지도록 학습하는 방법이다. 가중치 값을 작게 하여 오버피팅을 일어나지 않게 한다. 가중치를 작게 만들고 싶으면 초깃값도 최대한 작은 값에서 시작해야한다. 하지만 가중치의 초깃값을 모두 0으로 설정하면 학습이 올바르게 이루어지지 않는다. 왜냐하면 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문이다.
은닉층의 활성화값 분포
은니긍의 활성화값의 분포를 관찰하면 중요한 정보를 얻을 수 있다. 구체적으로 활성화 함수로 시그모이드 함수를 사용하는 5층 신경망에 무작위로 생성한 입력 데이터를 통해 각 층의 활성화 값 분포를 그려보자.
import numpy as np
import matplotlib.pyplot as plt
from functions import *
import warnings
warnings.filterwarnings('ignore')
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) * 1
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
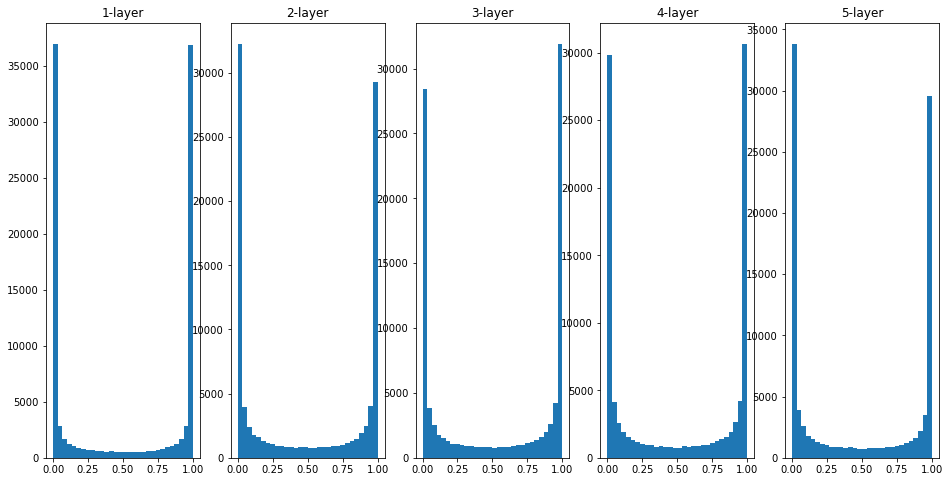
각 층의 활성화 값들은 0과 1에 치우쳐 분포되어 있다. 시그모이드 함수는 그 출력이 0에 가까워지면, 미분은 0에 다가간다. 따라서 데이터가 0과 1에 치우쳐 분포하게 되면 역전파의 기울기 값이 점점 작아지다가 사라지는 기울기 소실(gradient vanishing)문제가 발생한다. 가중치의 표준편차를 0.01로 바꿔 반복해보면
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) * 0.01
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
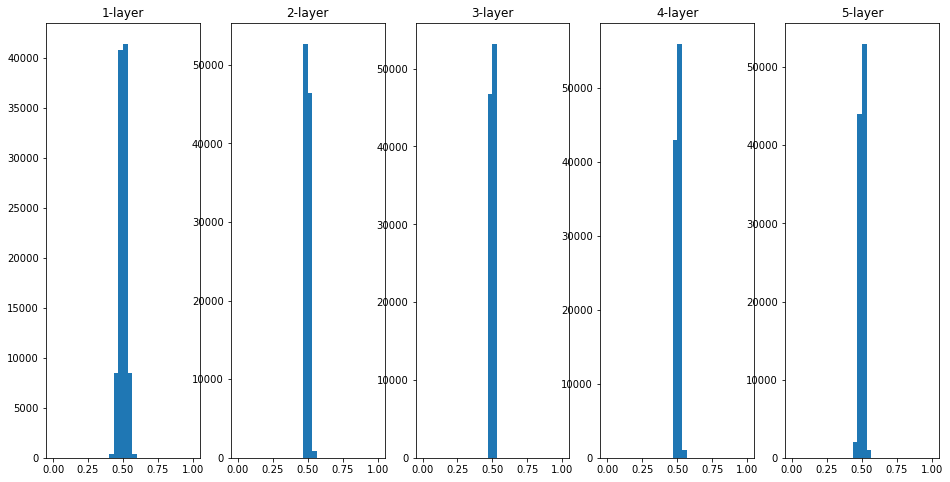
이번에는 0.5 부근에 집중되어있다. 기울기 소실 문제는 일어나지 않았지만, 활성화값들이 치우쳤다는 것은 표현력 관점에서 큰 문제가 있다. 즉 다수의 뉴런이 거의 같은 값을 추력하고 있으며 여러개의 뉴런이 의미가 없다는것을 의미한다. 따라서 표현력을 제한한다는 관점의 문제가 생긴다.
다음으로 Xavier 초깃값을 사용해보면, 앞 계층의 노드가 $n$개라면 표준편차가 $\frac{1}{\sqrt{n}}$인 분포를 사용하면 된다. Xavier 초깃값을 사용하면 앞 층에 노드가 많을수록 대상 노드의 초깃값으로 설정하는 가중치가 좁게 퍼진다.
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) / (np.sqrt(node_num))
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
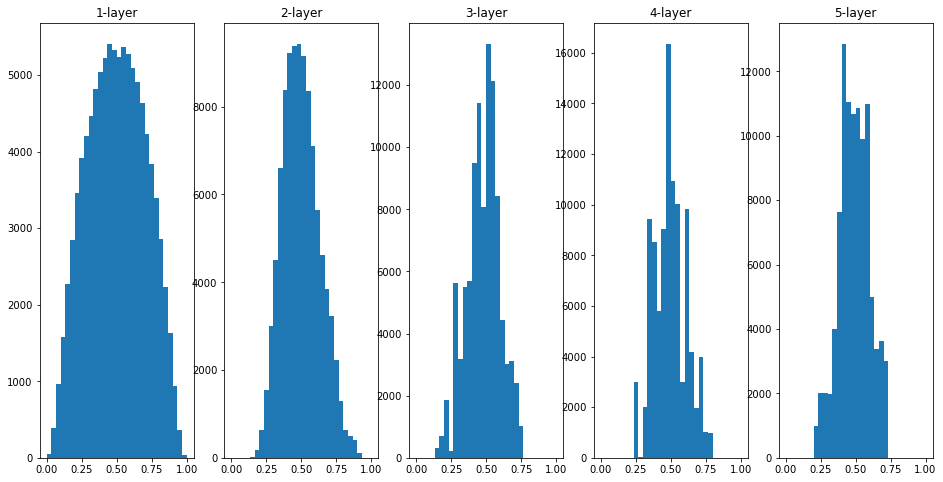
Xavier 초깃값을 사용하면 층이 깊어지면서 형태가 다소 일그러지지만, 활실히 넓게 분포하는걸 볼 수 있다. 시그모이드 함수의 표현력이 제한받지 않고 학습이 효율적으로 이뤄질 것으로 기대된다.
그래프는 오른쪽으로 갈수록 약간씩 일그러지고 있다. 이 일그러짐은 Sigmoid 함수 대신 tanh 함수를 이용하면 개선된다. tanh함수는 원점에서 대칭인 곡선인 반면, sigmoid 함수는 (0, 0.5)에서 대칭인 S곡선이기 때문에 발생한다.
def tanh(x):
return (np.exp(x)-np.exp(-x)) / (np.exp(x) + np.exp(-x))
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) / (np.sqrt(node_num))
a = np.dot(x, w)
z = tanh(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
ReLU를 사용할 때의 가중치 초깃값
ReLU에 특화된 초깃값은 He 초기값이라고 한다. ReLU는 음의 영역이 0이라서 더 넓게 분포시키기 위해 2배의 계수가 필요하다고 해석할 수 있다.
Xavier 초깃값 사용
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) / (np.sqrt(node_num))
a = np.dot(x, w)
z = relu(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
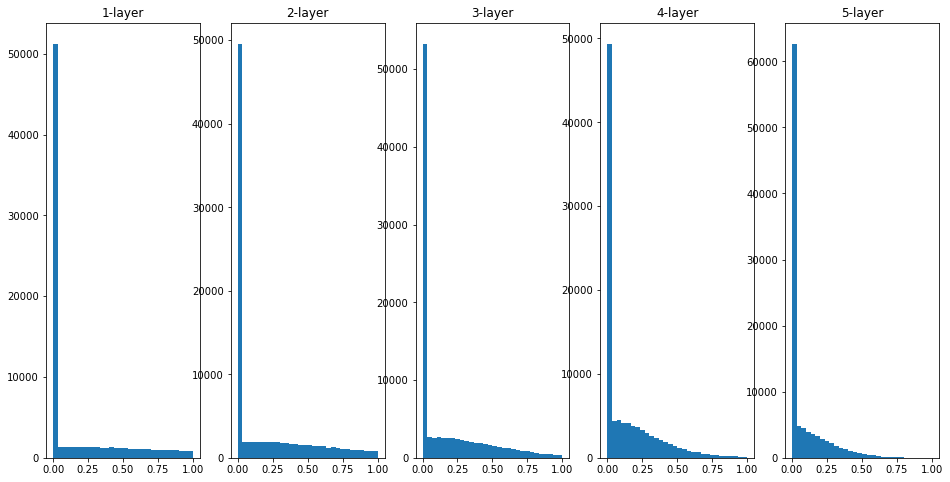
He 초깃값 사용
x = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) / np.sqrt(node_num / 2)
a = np.dot(x, w)
z = relu(a)
activations[i] = z
plt.figure(figsize=(16, 8))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + '-layer')
plt.hist(a.flatten(), 30, range=(0, 1))
plt.show()
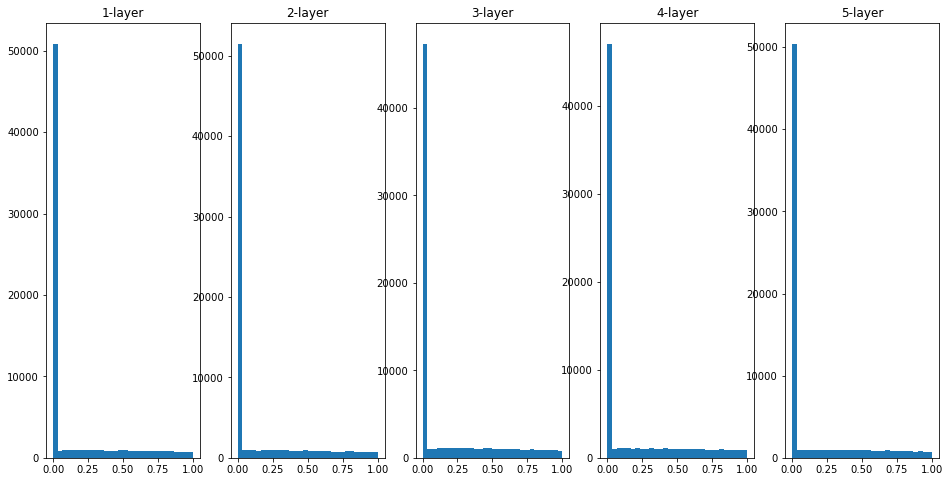
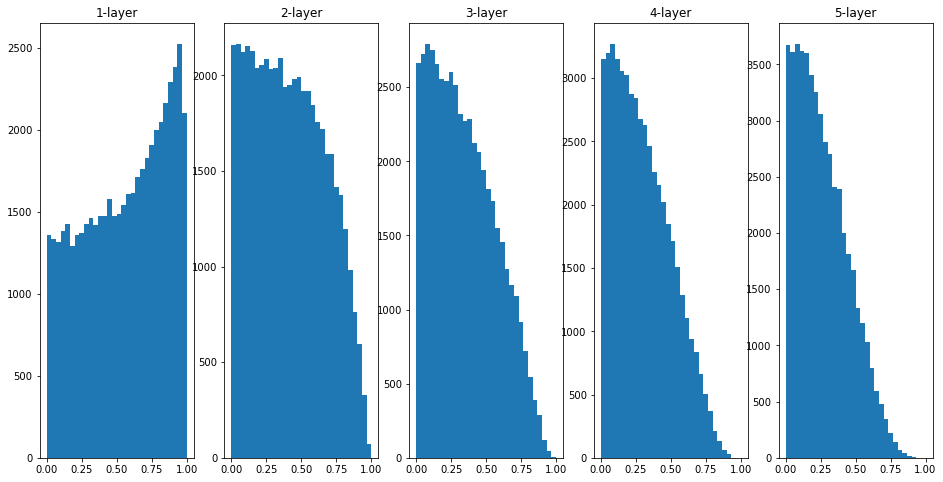
Xavier 초깃값을 사용했을 경우, 층이 깊어지면서 치우침이 조금씩 커진다. 실제로 층이 깊어지면 활성화값들의 치우침도 커지고, 학습할 때 기울기 소실 문제를 일으킨다. He 초갓값은 층이 깊어져도 분포가 균일하게 유지되기에 역전파 때도 적절한 값이 나올것으로 기대할 수 있다.
MNIST
import numpy as np
import matplotlib.pyplot as plt
from dataset import load_mnist
from util import smooth_curve
from multi_layer_net import MultiLayerNet
from optimizer import SGD
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
# if i % 100 == 0:
# print("===========" + "iteration:" + str(i) + "===========")
# for key in weight_init_types.keys():
# loss = networks[key].loss(x_batch, t_batch)
# print(key + ":" + str(loss))
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()
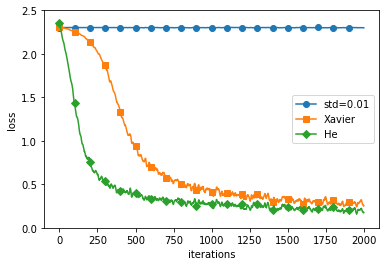
Batch Normalization
배치정규화의 장점으로는
- 학습 속도 개선
- 초깃값에 크게 의존하지 않는다.
- 오버피팅을 억제한다.(드롭아웃의 필요성 감소)
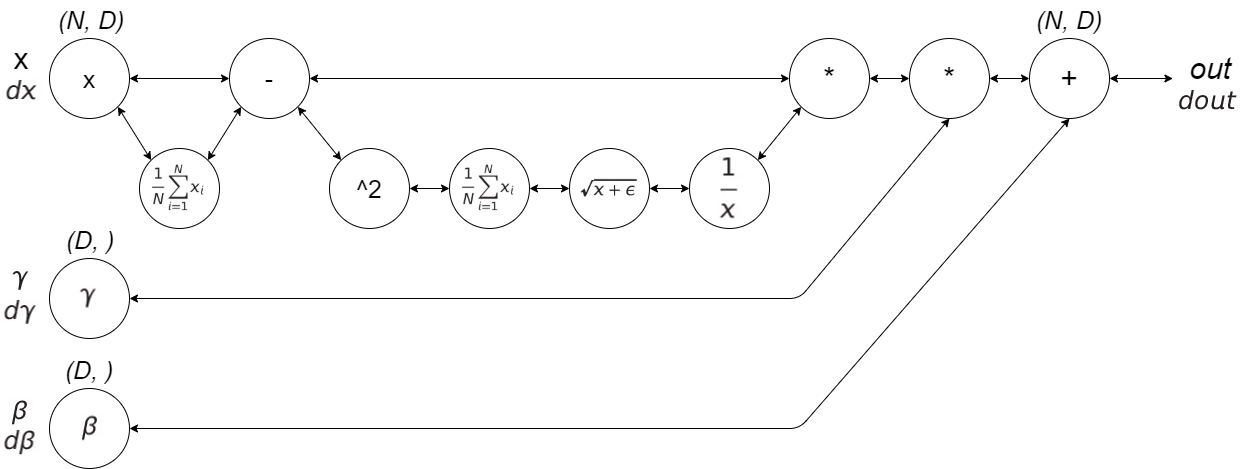
배치정규화는 각 층에서의 활성화값이 적당히 분포되도록 조정하는것이다. 따라서 데이터 분포를 정규화하는 ‘Batch Norm 계층’을 신경망에 삽입한다.
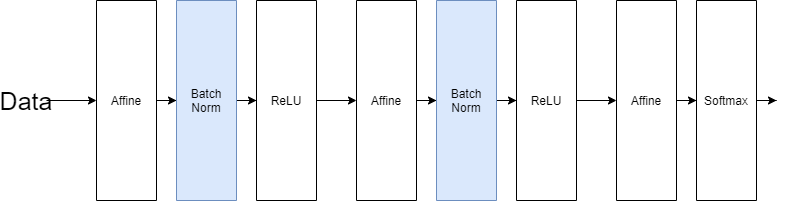
배치 정규화는 학습 시 미니배치를 단위로 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화한다.
$\mu_{B} \leftarrow \frac{1}{M} \sum_{i=1}^{m} x_{i}$
$\sigma_{B}^{2} \leftarrow \frac{1}{M} \sum_{i=1}^{m} (x_{i} - \mu_{B})^{2}$
$\hat{x_{i}} \leftarrow \frac{x_{i} - \sigma_{B}}{\sqrt{\sigma_{B}^{2} + \epsilon}}$
여기에서 $\epsilon$은 작은 값으로, 0으로 나누는 사태를 예방한다.
또, 배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대와 이동 변환을 수행한다.
$y_{i} \leftarrow \gamma \hat{x_|{i}} + \beta$
이 식에서 $\gamma$가 확대를, $\beta$가 이동을 담당한다. 두 값은 처음에는 $\gamma = 1, \beta = 0$부터 시작하고, 학습하면서 적절한 값으로 조정된다.
from multi_layer_net_extend import MultiLayerNetExtend
from optimizer import SGD, Adam
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
x_train = x_train[:1000]
t_train = t_train[:1000]
max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
def __train(weight_init_std):
bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std, use_batchnorm=True)
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std)
optimizer = SGD(lr=learning_rate)
train_acc_list = []
bn_train_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for _network in (bn_network, network):
grads = _network.gradient(x_batch, t_batch)
optimizer.update(_network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
bn_train_acc = bn_network.accuracy(x_train, t_train)
train_acc_list.append(train_acc)
bn_train_acc_list.append(bn_train_acc)
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
return train_acc_list, bn_train_acc_list
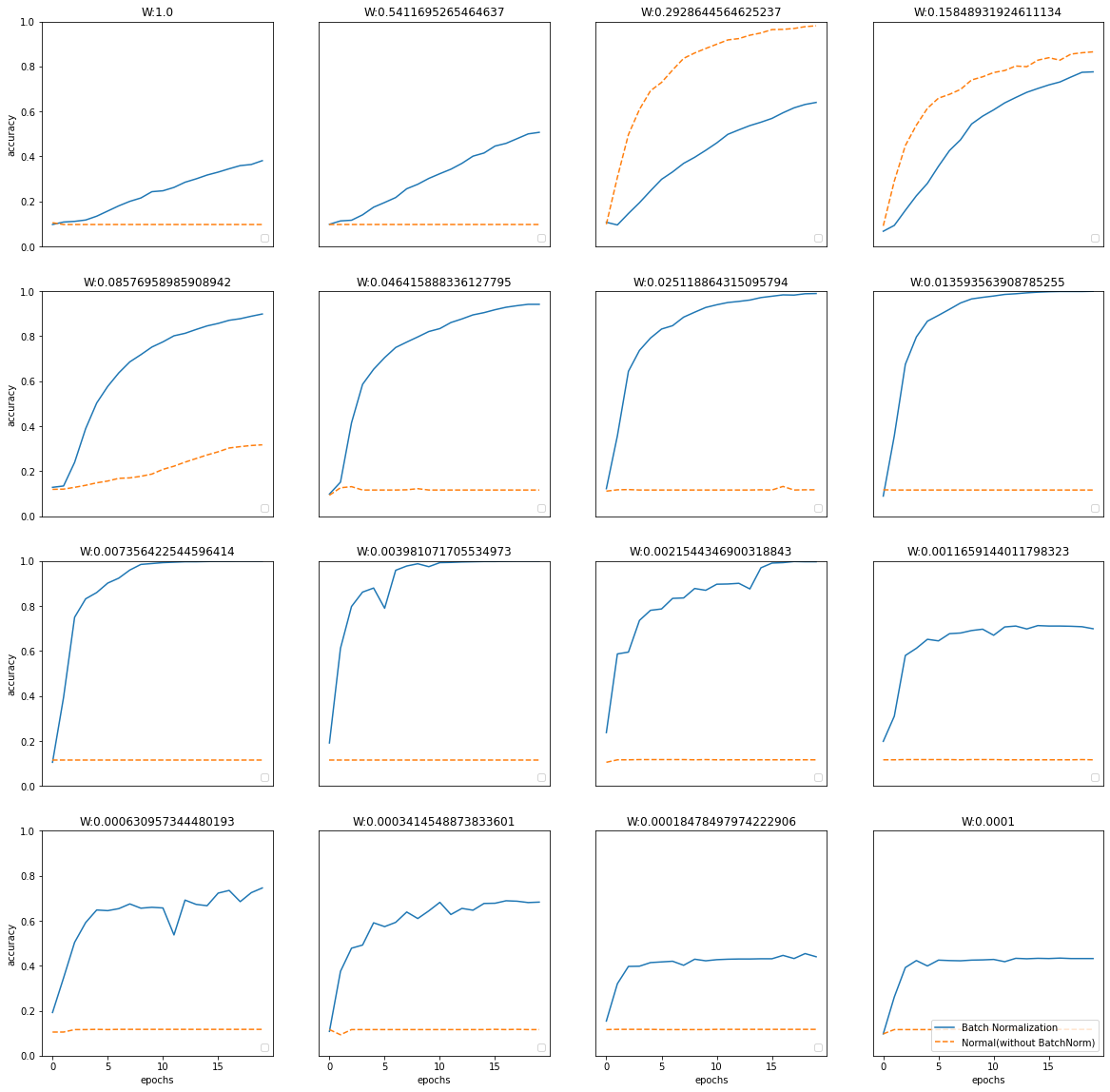
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)
plt.figure(figsize=(20,20))
for i, w in enumerate(weight_scale_list):
train_acc_list, bn_train_acc_list = __train(w)
plt.subplot(4,4,i+1)
plt.title("W:" + str(w))
if i == 15:
plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
else:
plt.plot(x, bn_train_acc_list, markevery=2)
plt.plot(x, train_acc_list, linestyle="--", markevery=2)
plt.ylim(0, 1.0)
if i % 4:
plt.yticks([])
else:
plt.ylabel("accuracy")
if i < 12:
plt.xticks([])
else:
plt.xlabel("epochs")
plt.legend(loc='lower right')
plt.show()
참고 : 사이토 고키, 『DeepLearning from Scratch』, 한빛미디어(2020), 190-214