Deep Learning from Scratch - Training Skills(1)
Optimization
SGD(Stochastic Gradient Descent)
여기에서 $W$는 갱신할 가중치 매개변수이며, $\frac{\partial L}{\partial W}$은 $W$에 대한 손실 함수의 깅루기이다. $\eta$는 학습률을 의미하는데, 0.01이나 0.001과 같은 값을 미리 정해서 사용한다.
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
class SGD:
def __init__(self, lr = 0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
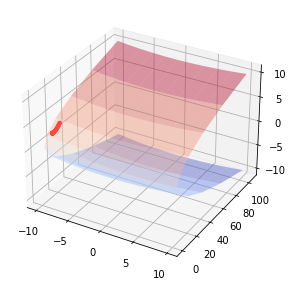
SGD는 단순하고 구현도 쉽지만, 문제에 따라서는 비효율적이다. 비등방성 함수의 경우 탐색 경로가 비효율적이다.
$f(x,y) = \frac{1}{20}x^{2} + y^{2}$
def fxy(x, y):
return x**2 / 20 + y**2
def dfx(x, y):
return x / 10 + y**2
def dfy(x, y):
return x**2 / 20 + 2 * y
lr = 0.01
max_iter = 1000
initial = np.array([-7, 2])
answer = initial.reshape(1, 2)
for n in range(max_iter):
gradient_x = dfx(initial[0], initial[1])
gradient_y = dfx(initial[0], initial[1])
gradients = np.array([gradient_x, gradient_y])
initial = initial - lr * gradients
answer = np.concatenate((answer, initial.reshape(1,2)), axis=0)
if initial[0] < 0.0000001 and initial[1] < 0.0000001:
break
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = np.linspace(-10, 10, 11)
X = np.tile(x, (11, 1))
Y = np.transpose(X)
Z = fxy(X, Y)
ax.plot_surface(X, Z, Y, cmap=cm.coolwarm, alpha=0.4)
ax.scatter(answer[:, 0], answer[:, 1], fxy(answer[:,0], answer[:,1]), s=10, c='r')
plt.tight_layout()
plt.show()
Momentum
여기서 $\nu$는 속도에 해당한다. 즉 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙을 나타낸다.
class Momentum:
def __init__(self, lr = 0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
AdaGrad
Learning Rate($\eta$)의 값이 너무 작으면 학습 시간이 너무 길어지며, 반대로 너무 크면 발산하여 학습이 잘 이루어지지 않는다. 이것을 정하는 기술로 learning rate decay가 있다. 처음에는 크게 학습하다가 조금씩 작게 학습한다. 학습률을 서서히 낮추는 가장 간단한 방법은 매개변수 전체의 학습률 값을 일괄적으로 낮추는것이며 이를 발전시킨것이 AdaGrad이다.
$h \leftarrow h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W}$
$W \leftarrow W - \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W}$
여기서 $h$는 기존 기울기 값을 제곱하여 계속 더해준다. 그리고 매개변수를 갱신할 때 $\frac{1}{\sqrt{h}}$을 곱해 학습률을 조정해준다. 즉 매개변수의 원소 중에서 많이 움직인(크게 갱신된) 원소는 학습률이 낮아진다는 뜻이며, 학습률 감소가 매개변수의 원소마다 다르게 적용됨을 뜻한다.
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
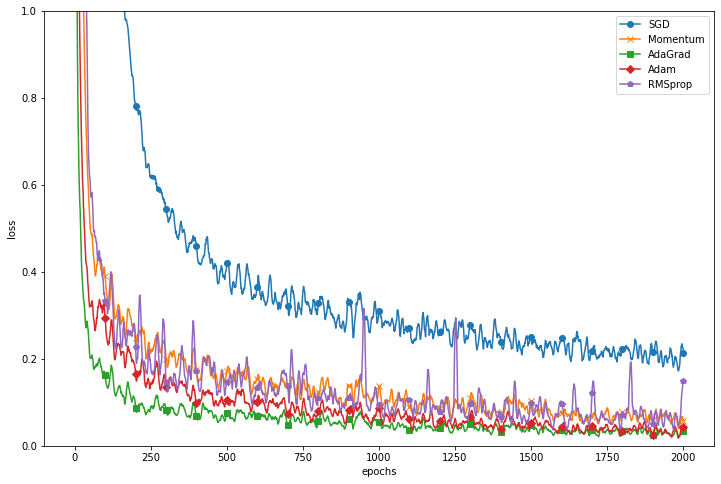
Optimizer Compare
import matplotlib.pyplot as plt
from dataset import load_mnist
from optimizer import *
from multi_layer_net import MultiLayerNet
from util import smooth_curve
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
epochs = 2000
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(input_size=784,
hidden_size_list = [100, 100, 100, 100],
output_size = 10)
train_loss[key] = []
for i in range(epochs+1):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print('=====' + 'epoch:' + str(i) + '=====')
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ':' + str(loss))
print('\n')
=====epoch:0=====
SGD:2.323933561248506
Momentum:2.363245841817952
AdaGrad:2.0058678291110414
Adam:2.2334862629381247
RMSprop:14.22925630514287
=====epoch:100=====
SGD:1.5642248269340318
Momentum:0.38734450281445537
AdaGrad:0.17621693935291363
Adam:0.29530935596559615
RMSprop:0.27206693914231306
=====epoch:200=====
SGD:0.686122412862151
Momentum:0.15622272140572271
AdaGrad:0.06336690000897913
Adam:0.11336671915710754
RMSprop:0.17646344103478384
=====epoch:300=====
SGD:0.4545903408140268
Momentum:0.19771072117917854
AdaGrad:0.07949768723147957
Adam:0.09508616556545395
RMSprop:0.12008675039395529
=====epoch:400=====
SGD:0.4888092137718686
Momentum:0.16832245932781956
AdaGrad:0.08314873345194046
Adam:0.10753427697857422
RMSprop:0.16275149688659427
=====epoch:500=====
SGD:0.41182912871414307
Momentum:0.16891254992386134
AdaGrad:0.09577087646405533
Adam:0.13343288513695772
RMSprop:0.1509381717316755
=====epoch:600=====
SGD:0.38457191195719936
Momentum:0.17943574810854546
AdaGrad:0.0956186384355422
Adam:0.13159736035092054
RMSprop:0.21822940306148478
=====epoch:700=====
SGD:0.23862203822432784
Momentum:0.10301943877274536
AdaGrad:0.02559461765057868
Adam:0.06254043615993003
RMSprop:0.13542406013915123
=====epoch:800=====
SGD:0.29539795679444475
Momentum:0.16795679782037173
AdaGrad:0.06100571581620096
Adam:0.10210300999031789
RMSprop:0.12895927515125238
=====epoch:900=====
SGD:0.4140718396219327
Momentum:0.16519305717420346
AdaGrad:0.06692166063208266
Adam:0.07957113805987726
RMSprop:0.13062510151653964
=====epoch:1000=====
SGD:0.3515850025553312
Momentum:0.07630399868811209
AdaGrad:0.035831266442459486
Adam:0.031605081665158505
RMSprop:0.08687585855353055
=====epoch:1100=====
SGD:0.27671053746498353
Momentum:0.0927991189334633
AdaGrad:0.03429342415567612
Adam:0.06404277656831128
RMSprop:0.10490014031616401
=====epoch:1200=====
SGD:0.31741957526083986
Momentum:0.1123296449397075
AdaGrad:0.04982732116821773
Adam:0.062178961376442084
RMSprop:0.13679383222548375
=====epoch:1300=====
SGD:0.2292543596026353
Momentum:0.06967261211484445
AdaGrad:0.03302473628750588
Adam:0.05636652638864118
RMSprop:0.09318564993538125
=====epoch:1400=====
SGD:0.22237756148390314
Momentum:0.04882674904268745
AdaGrad:0.028742998382779012
Adam:0.015687868869984772
RMSprop:0.04109031955332386
=====epoch:1500=====
SGD:0.28039821371170026
Momentum:0.15725926811597074
AdaGrad:0.06663606677806189
Adam:0.07872465833141339
RMSprop:0.1811693993698395
=====epoch:1600=====
SGD:0.18627340858169092
Momentum:0.09531247495270898
AdaGrad:0.06224859468860602
Adam:0.036661451686031306
RMSprop:0.13888397442464653
=====epoch:1700=====
SGD:0.2345269210359547
Momentum:0.07508226021236863
AdaGrad:0.04970229707152042
Adam:0.07056549755653727
RMSprop:0.1535827013299852
=====epoch:1800=====
SGD:0.17507715717516453
Momentum:0.07569051309421965
AdaGrad:0.03774834237742847
Adam:0.026715994596425666
RMSprop:0.026451178822442755
=====epoch:1900=====
SGD:0.23511866141021298
Momentum:0.09448058945525774
AdaGrad:0.022293080750721103
Adam:0.02513916870501018
RMSprop:0.032113769609402695
=====epoch:2000=====
SGD:0.2229854127826571
Momentum:0.05897965953558401
AdaGrad:0.02959130337156857
Adam:0.03409000704065028
RMSprop:0.15438018030242323
markers = {'SGD': 'o', 'Momentum': 'x', 'AdaGrad' : 's', 'Adam': 'D','RMSprop':'p'}
x = np.arange(epochs+1)
plt.figure(figsize=(12,8))
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100,
label = key)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.ylim(0, 1)
plt.legend()
plt.show()
참고 : 사이토 고키, 『DeepLearning from Scratch』, 한빛미디어(2020), p189-202