/ TIMESERIES

Time Series Analysis - General Forecasting Model

Introduction to Forecasting

import pandas as pd
import numpy as np
%matplotlib inline

df = pd.read_csv('Data/airline_passengers.csv',index_col = 'Month', parse_dates=True)

df.index.freq = 'MS'

df.head()
Thousands of Passengers
Month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121 
df.tail()
Thousands of Passengers
Month
1960-08-01 606
1960-09-01 508
1960-10-01 461
1960-11-01 390
1960-12-01 432
  • The size of the test set is typically about 20% of the total sample, although this value depends on how long the sample is and how far ahead you want to forecast. The test set should ideally be at least as large as the maximum forecast horizon required.
  • Keep in mind, the longer the forecast horizon, the more likely your prediction becomes less accurate
df.info()

<class 'pandas.core.frame.DataFrame'>
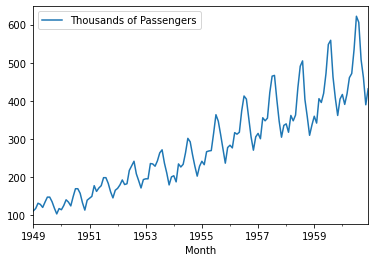
DatetimeIndex: 144 entries, 1949-01-01 to 1960-12-01
Freq: MS
Data columns (total 1 columns):
 #   Column                   Non-Null Count  Dtype
---  ------                   --------------  -----
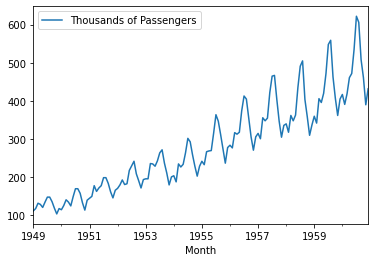
 0   Thousands of Passengers  144 non-null    int64
dtypes: int64(1)
memory usage: 2.2 KB

train_data = df.iloc[:109] #.loc[:'1940-01-01']
test_data = df.iloc[108:]

from statsmodels.tsa.holtwinters import ExponentialSmoothing

fitted_model = ExponentialSmoothing(train_data['Thousands of Passengers'],
                                   trend='mul',seasonal='mul',
                                   seasonal_periods=12).fit()

C:\Users\ilvna\.conda\envs\tf-2.3\lib\site-packages\statsmodels\tsa\holtwinters\model.py:429: FutureWarning: After 0.13 initialization must be handled at model creation
  FutureWarning,
C:\Users\ilvna\.conda\envs\tf-2.3\lib\site-packages\statsmodels\tsa\holtwinters\model.py:80: RuntimeWarning: overflow encountered in matmul
  return err.T @ err

test_predictions = fitted_model.forecast(36)

test_predictions

1958-02-01    339.142839
1958-03-01    399.281567
1958-04-01    394.233518
1958-05-01    402.545212
1958-06-01    473.128729
1958-07-01    521.795258
1958-08-01    514.513564
1958-09-01    446.216722
1958-10-01    385.430842
1958-11-01    339.645012
1958-12-01    381.455551
1959-01-01    401.210071
1959-02-01    387.159060
1959-03-01    455.812296
1959-04-01    450.049538
1959-05-01    459.538011
1959-06-01    540.114821
1959-07-01    595.671611
1959-08-01    587.358966
1959-09-01    509.392582
1959-10-01    440.000570
1959-11-01    387.732331
1959-12-01    435.462452
1960-01-01    458.013840
1960-02-01    441.973470
1960-03-01    520.346708
1960-04-01    513.768052
1960-05-01    524.599914
1960-06-01    616.584878
1960-07-01    680.007460
1960-08-01    670.517902
1960-09-01    581.512951
1960-10-01    502.296340
1960-11-01    442.627906
1960-12-01    497.115710
1961-01-01    522.859949
Freq: MS, dtype: float64

train_data['Thousands of Passengers'].plot(legend=True, label='TRAIN',figsize=(12,8))
test_data['Thousands of Passengers'].plot(legend=True, label='TEST')

<AxesSubplot:xlabel='Month'>

png

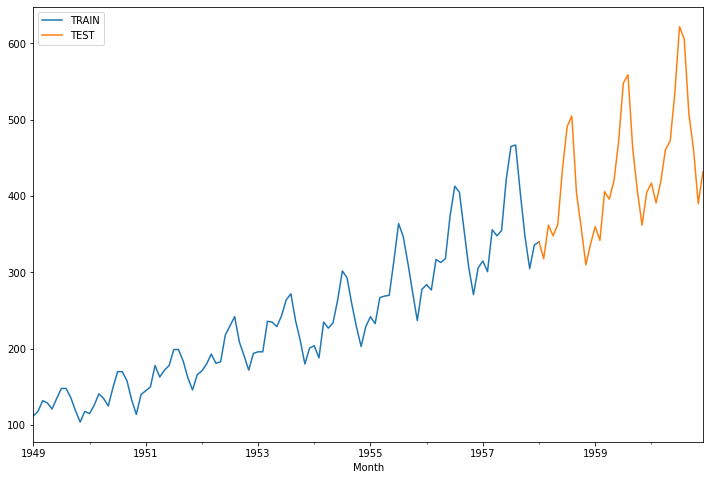
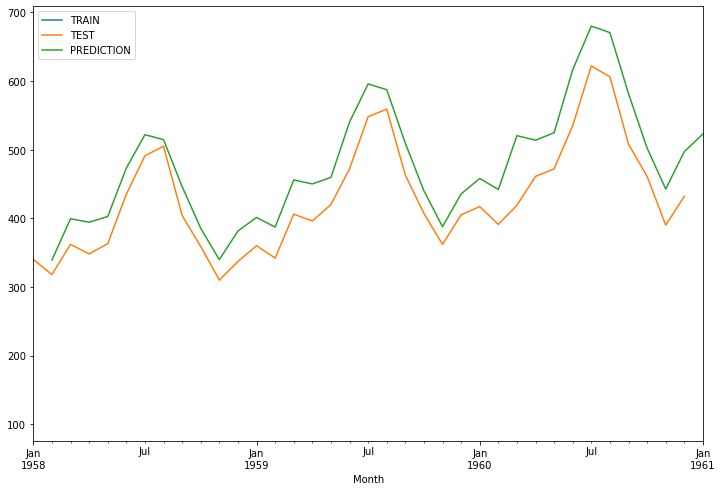
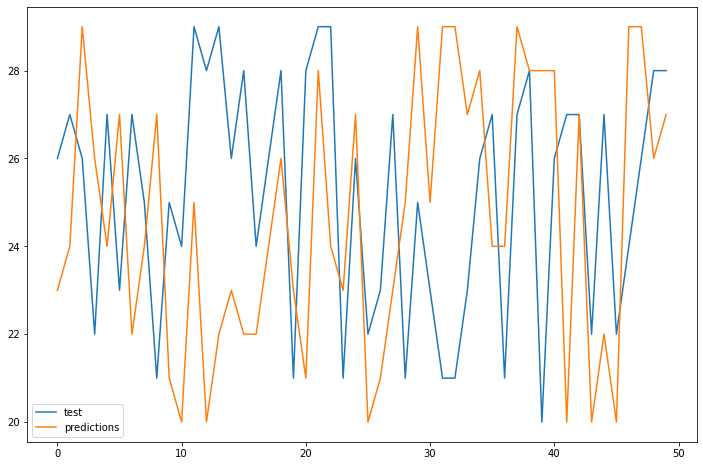
train_data['Thousands of Passengers'].plot(legend=True, label='TRAIN',figsize=(12,8))
test_data['Thousands of Passengers'].plot(legend=True, label='TEST')
test_predictions.plot(legend=True, label='PREDICTION',xlim=['1958-01-01','1961-01-01'])

<AxesSubplot:xlabel='Month'>

png

from sklearn.metrics import mean_absolute_error, mean_squared_error

test_data.describe()
Thousands of Passengers
count 36.000000
mean 428.500000
std 79.329152
min 310.000000
25% 362.000000
50% 412.000000
75% 472.000000
max 622.000000 
mean_absolute_error(test_data, test_predictions)

63.031111382769595

mean_squared_error(test_data, test_predictions)

5614.2515044341835

np.sqrt(mean_squared_error(test_data,test_predictions))

74.92830909899264

final_model = ExponentialSmoothing(df['Thousands of Passengers'], trend ='mul',seasonal='mul',seasonal_periods=12).fit()

C:\Users\ilvna\.conda\envs\tf-2.3\lib\site-packages\statsmodels\tsa\holtwinters\model.py:429: FutureWarning: After 0.13 initialization must be handled at model creation
  FutureWarning,
C:\Users\ilvna\.conda\envs\tf-2.3\lib\site-packages\statsmodels\tsa\holtwinters\model.py:80: RuntimeWarning: overflow encountered in matmul
  return err.T @ err

forecast_prediction = final_model.forecast(36)

df['Thousands of Passengers'].plot(figsize=(12,8))
forecast_prediction.plot()

<AxesSubplot:xlabel='Month'>

png

df2 = pd.read_csv('Data/samples.csv', index_col = 0, parse_dates=True)

df2.head()
a b c d
1950-01-01 36 27 0 67
1950-02-01 58 22 3 31
1950-03-01 61 17 5 67
1950-04-01 37 15 8 47
1950-05-01 66 13 8 62 
df2['a'].plot()

<AxesSubplot:>

png

df2['b'].plot()

<AxesSubplot:>

png

from statsmodels.tsa.statespace.tools import diff

# df2['b'] - df2['b'].shift(1)
diff(df2['b'], k_diff=1).plot()

<AxesSubplot:>

png

ACF & PACF

import pandas as pd
import numpy as np
%matplotlib inline

import statsmodels.api as sm

from statsmodels.tsa.stattools import acovf, acf, pacf, pacf_yw, pacf_ols

# NON STATIONARY
df1 = pd.read_csv('Data/airline_passengers.csv',index_col='Month', parse_dates=True)
df1.index.freq = 'MS'

# STATIONARY
df2 = pd.read_csv('Data/DailyTotalFemaleBirths.csv', index_col='Date', parse_dates=True)
df2.index.freq = 'D'

df1.head()
Thousands of Passengers
Month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121 
df2.head()
Births
Date
1959-01-01 35
1959-01-02 32
1959-01-03 30
1959-01-04 31
1959-01-05 44 
import warnings
warnings.filterwarnings('ignore')

df = pd.DataFrame({'a' : [13, 5, 11, 12, 9]})

df
a
0 13
1 5
2 11
3 12
4 9 
acf(df['a'])

array([ 1.   , -0.5  , -0.2  ,  0.275, -0.075])

pacf_yw(df['a'], nlags=4, method='unbiased')

array([ 1.        , -0.625     , -1.18803419,  2.03764205,  0.8949589 ])

pacf_ols(df['a'], nlags=4)

array([ 1.        , -0.49677419, -0.43181818,  0.53082621,  0.25434783])

from pandas.plotting import lag_plot

lag_plot(df1['Thousands of Passengers'])

<AxesSubplot:xlabel='y(t)', ylabel='y(t + 1)'>

png

lag_plot(df2['Births'])

<AxesSubplot:xlabel='y(t)', ylabel='y(t + 1)'>

png

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(df1,lags=40);

png

plot_acf(df2, lags=40);

png

plot_pacf(df2, lags=40, title='Daily Female Births');

png

ARIMA

import pandas as pd
import numpy as np
%matplotlib inline

from statsmodels.tsa.ar_model import AR, ARResults

df = pd.read_csv('Data/uspopulation.csv', index_col='DATE', parse_dates=True)

df.index.freq = 'MS'

df.head()
PopEst
DATE
2011-01-01 311037
2011-02-01 311189
2011-03-01 311351
2011-04-01 311522
2011-05-01 311699 
df.plot(figsize = (12, 8))

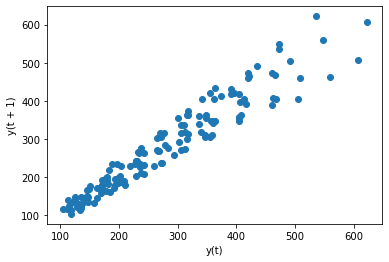
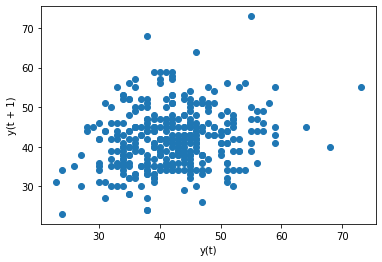
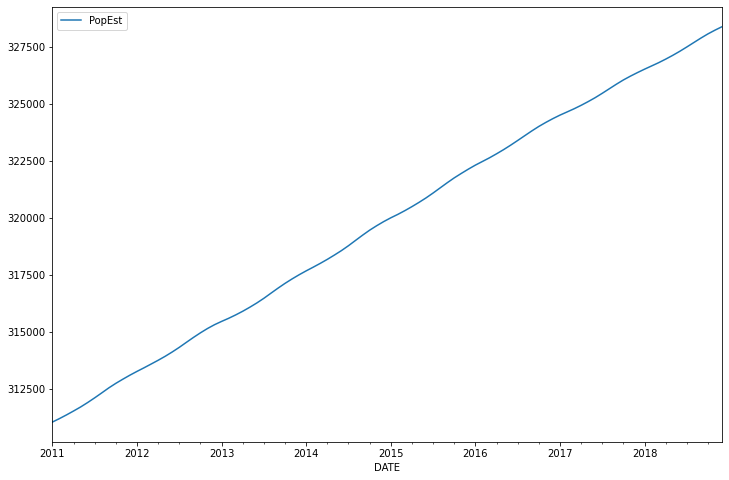
<AxesSubplot:xlabel='DATE'>

png

len(df)

96

96-12

84

train = df.iloc[:84]
test = df.iloc[84:]

import warnings
warnings.filterwarnings('ignore')

model = AR(train['PopEst'])

AR1fit = model.fit(maxlag=1)

AR1fit.k_ar

1

AR1fit.params

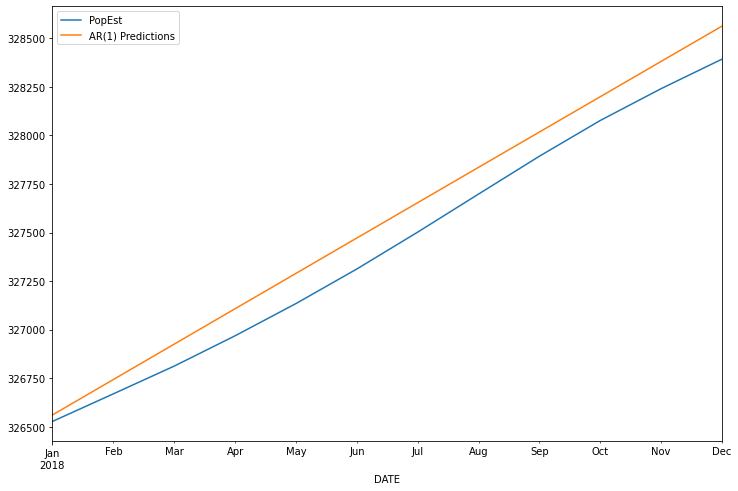
const        284.913797
L1.PopEst      0.999686
dtype: float64

start = len(train)
end = len(train) + len(test) - 1

print(start, end)

84 95

AR1fit.predict(start, end)

2018-01-01    326560.403377
2018-02-01    326742.749463
2018-03-01    326925.038278
2018-04-01    327107.269838
2018-05-01    327289.444162
2018-06-01    327471.561268
2018-07-01    327653.621173
2018-08-01    327835.623896
2018-09-01    328017.569455
2018-10-01    328199.457868
2018-11-01    328381.289152
2018-12-01    328563.063326
Freq: MS, dtype: float64

test
PopEst
DATE
2018-01-01 326527
2018-02-01 326669
2018-03-01 326812
2018-04-01 326968
2018-05-01 327134
2018-06-01 327312
2018-07-01 327502
2018-08-01 327698
2018-09-01 327893
2018-10-01 328077
2018-11-01 328241
2018-12-01 328393 
predictions1 = AR1fit.predict(start, end)

predictions1 = predictions1.rename('AR(1) Predictions')

predictions1

2018-01-01    326560.403377
2018-02-01    326742.749463
2018-03-01    326925.038278
2018-04-01    327107.269838
2018-05-01    327289.444162
2018-06-01    327471.561268
2018-07-01    327653.621173
2018-08-01    327835.623896
2018-09-01    328017.569455
2018-10-01    328199.457868
2018-11-01    328381.289152
2018-12-01    328563.063326
Freq: MS, Name: AR(1) Predictions, dtype: float64

test.plot(figsize = (12,8), legend = True)
predictions1.plot(legend = True)

<AxesSubplot:xlabel='DATE'>

png

model = AR(train['PopEst'])

AR2fit = model.fit(maxlag = 2)

AR2fit.params

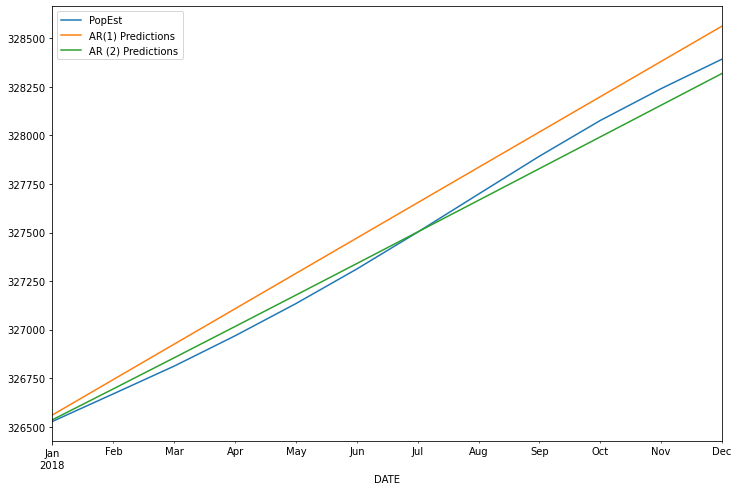
const        137.368305
L1.PopEst      1.853490
L2.PopEst     -0.853836
dtype: float64

predictions2 = AR2fit.predict(start, end)

predictions2 = predictions2.rename('AR (2) Predictions')

test.plot(figsize = (12,8), legend = True)
predictions1.plot(legend = True)
predictions2.plot(legend = True)

<AxesSubplot:xlabel='DATE'>

png

model = AR(train['PopEst'])

ARfit = model.fit(ic='t-stat')

ARfit.params

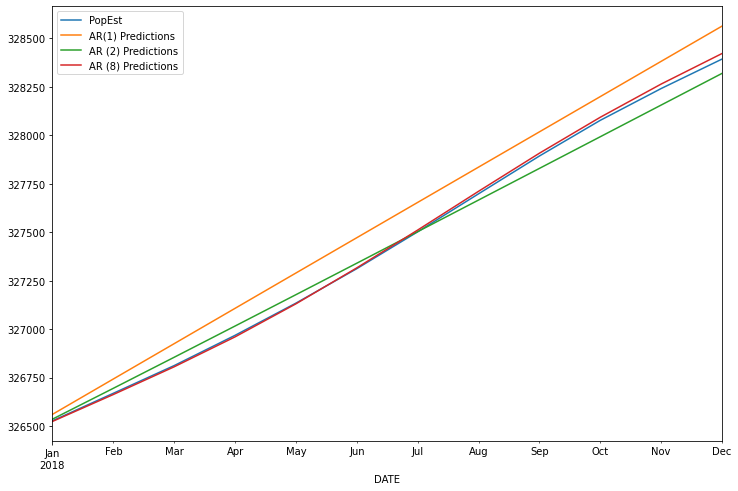
const        82.309677
L1.PopEst     2.437997
L2.PopEst    -2.302100
L3.PopEst     1.565427
L4.PopEst    -1.431211
L5.PopEst     1.125022
L6.PopEst    -0.919494
L7.PopEst     0.963694
L8.PopEst    -0.439511
dtype: float64

predictions8 = ARfit.predict(start, end)
predictions8 = predictions8.rename('AR (8) Predictions')

from sklearn.metrics import mean_squared_error

labels = ['AR1', 'AR2', 'AR8']

preds = [predictions1, predictions2, predictions8]

for i in range(3):
    # np.sqrt()
    error = mean_squared_error(test['PopEst'],preds[i])
    print(f'{labels[i]} MSE was : {error}')

AR1 MSE was : 17449.714239577344
AR2 MSE was : 2713.258615675103
AR8 MSE was : 186.97377437908688

test.plot(figsize = (12,8), legend = True)
predictions1.plot(legend = True)
predictions2.plot(legend = True)
predictions8.plot(legend = True)

<AxesSubplot:xlabel='DATE'>

png

# Forecasting __ Future

model = AR(df['PopEst'])

ARfit = model.fit()

forcasted_values = ARfit.predict(start = len(df), end = len(df) + 12).rename('Forecast')

df['PopEst'].plot(figsize = (12,8), legend= True)
forcasted_values.plot(legend = True)

<AxesSubplot:xlabel='DATE'>

png

Descriptive Statisics and Tests

import pandas as pd
import numpy as np
%matplotlib inline

import warnings
warnings.filterwarnings('ignore')

df1 = pd.read_csv('Data/airline_passengers.csv', index_col = 'Month', parse_dates = True)
df1.index.freq = 'MS'

df2 = pd.read_csv('Data/DailyTotalFemaleBirths.csv', index_col = 'Date', parse_dates = True)
df2.index.freq = 'D'

df1.plot()

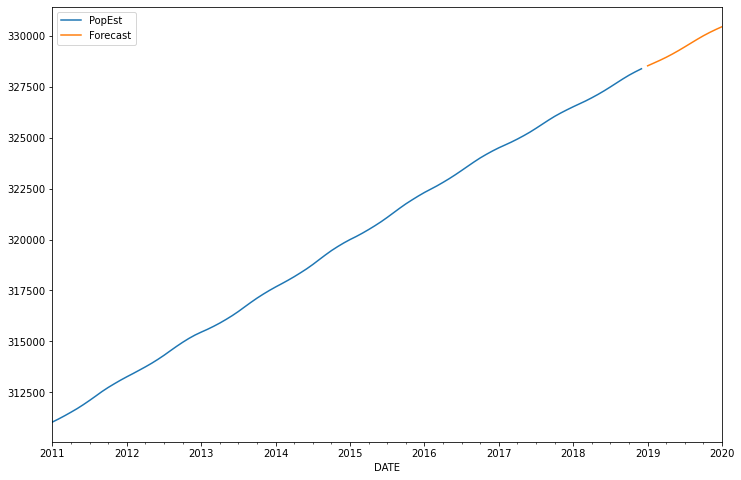
<AxesSubplot:xlabel='Month'>

png

from statsmodels.tsa.stattools import adfuller

adfuller(df1['Thousands of Passengers'])

(0.8153688792060512,
 0.991880243437641,
 13,
 130,
 {'1%': -3.4816817173418295,
  '5%': -2.8840418343195267,
  '10%': -2.578770059171598},
 996.692930839019)

help(adfuller)

Help on function adfuller in module statsmodels.tsa.stattools:

adfuller(x, maxlag=None, regression='c', autolag='AIC', store=False, regresults=False)
    Augmented Dickey-Fuller unit root test.
    
    The Augmented Dickey-Fuller test can be used to test for a unit root in a
    univariate process in the presence of serial correlation.
    
    Parameters
    ----------
    x : array_like, 1d
        The data series to test.
    maxlag : int
        Maximum lag which is included in test, default 12*(nobs/100)^{1/4}.
    regression : {"c","ct","ctt","nc"}
        Constant and trend order to include in regression.
    
        * "c" : constant only (default).
        * "ct" : constant and trend.
        * "ctt" : constant, and linear and quadratic trend.
        * "nc" : no constant, no trend.
    
    autolag : {"AIC", "BIC", "t-stat", None}
        Method to use when automatically determining the lag.
    
        * if None, then maxlag lags are used.
        * if "AIC" (default) or "BIC", then the number of lags is chosen
          to minimize the corresponding information criterion.
        * "t-stat" based choice of maxlag.  Starts with maxlag and drops a
          lag until the t-statistic on the last lag length is significant
          using a 5%-sized test.
    store : bool
        If True, then a result instance is returned additionally to
        the adf statistic. Default is False.
    regresults : bool, optional
        If True, the full regression results are returned. Default is False.
    
    Returns
    -------
    adf : float
        The test statistic.
    pvalue : float
        MacKinnon"s approximate p-value based on MacKinnon (1994, 2010).
    usedlag : int
        The number of lags used.
    nobs : int
        The number of observations used for the ADF regression and calculation
        of the critical values.
    critical values : dict
        Critical values for the test statistic at the 1 %, 5 %, and 10 %
        levels. Based on MacKinnon (2010).
    icbest : float
        The maximized information criterion if autolag is not None.
    resstore : ResultStore, optional
        A dummy class with results attached as attributes.
    
    Notes
    -----
    The null hypothesis of the Augmented Dickey-Fuller is that there is a unit
    root, with the alternative that there is no unit root. If the pvalue is
    above a critical size, then we cannot reject that there is a unit root.
    
    The p-values are obtained through regression surface approximation from
    MacKinnon 1994, but using the updated 2010 tables. If the p-value is close
    to significant, then the critical values should be used to judge whether
    to reject the null.
    
    The autolag option and maxlag for it are described in Greene.
    
    References
    ----------
    .. [1] W. Green.  "Econometric Analysis," 5th ed., Pearson, 2003.
    
    .. [2] Hamilton, J.D.  "Time Series Analysis".  Princeton, 1994.
    
    .. [3] MacKinnon, J.G. 1994.  "Approximate asymptotic distribution functions for
        unit-root and cointegration tests.  `Journal of Business and Economic
        Statistics` 12, 167-76.
    
    .. [4] MacKinnon, J.G. 2010. "Critical Values for Cointegration Tests."  Queen"s
        University, Dept of Economics, Working Papers.  Available at
        http://ideas.repec.org/p/qed/wpaper/1227.html
    
    Examples
    --------
    See example notebook

dftest = adfuller(df1['Thousands of Passengers'])
dfout = pd.Series(dftest[0:4], index = ['ADF Test Statistic','p-value','# Lags Used', '# Observations'])

for key, val in dftest[4].items():
    dfout[f'critical value ({key})'] = val

dfout

ADF Test Statistic        0.815369
p-value                   0.991880
# Lags Used              13.000000
# Observations          130.000000
critical value (1%)      -3.481682
critical value (5%)      -2.884042
critical value (10%)     -2.578770
dtype: float64

from statsmodels.tsa.stattools import adfuller

def adf_test(series, title=''):
    """
    Pass in a time series and an optional title, returns an ADF report
    """
    print(f'Augmented Dickey-Fuller Test: {title}')
    result = adfuller(series.dropna(), autolag = 'AIC')
    
    labels = ['ADF test statistic', 'p-value', '# lags used', '# obervations']
    out = pd.Series(result[0:4], index = labels)
    
    for key, val in result[4].items():
        out[f'critical value ({key})'] = val
        
    print(out.to_string())
    
    if result[1] <= 0.05:
        print('Strong evidence against the null hypothesis')
        print('Reject the null hypothesis')
        print('Data has no unit root and is stationary')
    else:
        print('Weak evidence against the null hypothesis')
        print('Fail to reject the null hypothesis')
        print('Data has a unit root and is non-stationary')

adf_test(df1['Thousands of Passengers'])

Augmented Dickey-Fuller Test: 
ADF test statistic        0.815369
p-value                   0.991880
# lags used              13.000000
# obervations           130.000000
critical value (1%)      -3.481682
critical value (5%)      -2.884042
critical value (10%)     -2.578770
Weak evidence against the null hypothesis
Fail to reject the null hypothesis
Data has a unit root and is non-stationary

df1.plot()

<AxesSubplot:xlabel='Month'>

png

df2.plot()

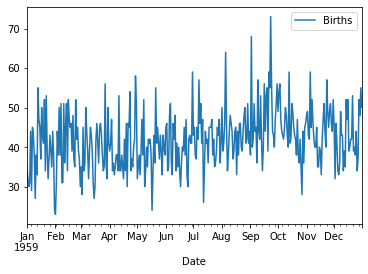
<AxesSubplot:xlabel='Date'>

png

adf_test(df2['Births'])

Augmented Dickey-Fuller Test: 
ADF test statistic       -4.808291
p-value                   0.000052
# lags used               6.000000
# obervations           358.000000
critical value (1%)      -3.448749
critical value (5%)      -2.869647
critical value (10%)     -2.571089
Strong evidence against the null hypothesis
Reject the null hypothesis
Data has no unit root and is stationary

df3 = pd.read_csv('Data/samples.csv', index_col = 0, parse_dates=True)
df3.index.freq = 'MS'

df3[['a','d']].plot(figsize = (12,8))

<AxesSubplot:>

png

df3['a'].iloc[2:].plot(figsize = (12,8), legend = True)
df3['d'].shift(2).plot(legend = True)

<AxesSubplot:>

png

from statsmodels.tsa.stattools import grangercausalitytests

grangercausalitytests(df3[['a','d']], maxlag = 3);

Granger Causality
number of lags (no zero) 1
ssr based F test:         F=1.7051  , p=0.1942  , df_denom=116, df_num=1
ssr based chi2 test:   chi2=1.7492  , p=0.1860  , df=1
likelihood ratio test: chi2=1.7365  , p=0.1876  , df=1
parameter F test:         F=1.7051  , p=0.1942  , df_denom=116, df_num=1

Granger Causality
number of lags (no zero) 2
ssr based F test:         F=286.0339, p=0.0000  , df_denom=113, df_num=2
ssr based chi2 test:   chi2=597.3806, p=0.0000  , df=2
likelihood ratio test: chi2=212.6514, p=0.0000  , df=2
parameter F test:         F=286.0339, p=0.0000  , df_denom=113, df_num=2

Granger Causality
number of lags (no zero) 3
ssr based F test:         F=188.7446, p=0.0000  , df_denom=110, df_num=3
ssr based chi2 test:   chi2=602.2669, p=0.0000  , df=3
likelihood ratio test: chi2=212.4789, p=0.0000  , df=3
parameter F test:         F=188.7446, p=0.0000  , df_denom=110, df_num=3

grangercausalitytests(df3[['b','d']], maxlag = 3);

Granger Causality
number of lags (no zero) 1
ssr based F test:         F=1.5225  , p=0.2197  , df_denom=116, df_num=1
ssr based chi2 test:   chi2=1.5619  , p=0.2114  , df=1
likelihood ratio test: chi2=1.5517  , p=0.2129  , df=1
parameter F test:         F=1.5225  , p=0.2197  , df_denom=116, df_num=1

Granger Causality
number of lags (no zero) 2
ssr based F test:         F=0.4350  , p=0.6483  , df_denom=113, df_num=2
ssr based chi2 test:   chi2=0.9086  , p=0.6349  , df=2
likelihood ratio test: chi2=0.9051  , p=0.6360  , df=2
parameter F test:         F=0.4350  , p=0.6483  , df_denom=113, df_num=2

Granger Causality
number of lags (no zero) 3
ssr based F test:         F=0.5333  , p=0.6604  , df_denom=110, df_num=3
ssr based chi2 test:   chi2=1.7018  , p=0.6365  , df=3
likelihood ratio test: chi2=1.6895  , p=0.6393  , df=3
parameter F test:         F=0.5333  , p=0.6604  , df_denom=110, df_num=3

np.random.seed(42)

df = pd.DataFrame(np.random.randint(20, 30,(50,2)), columns = ['test','predictions'])

df.head()
test predictions
0 26 23
1 27 24
2 26 29
3 22 26
4 27 24 
df.plot(figsize = (12,8))

<AxesSubplot:>

png

from statsmodels.tools.eval_measures import mse, rmse, meanabs

print(mse(df['test'], df['predictions']))
print(rmse(df['test'], df['predictions']))
print(meanabs(df['test'], df['predictions']))

17.02
4.125530268947253
3.54

df = pd.read_csv('Data/airline_passengers.csv', index_col='Month', parse_dates=True)
df.index.freq = 'MS'

df.plot()

<AxesSubplot:xlabel='Month'>

png

from statsmodels.graphics.tsaplots import month_plot, quarter_plot

month_plot(df['Thousands of Passengers']);

png

dfq = df['Thousands of Passengers'].resample(rule = 'Q').mean()

quarter_plot(dfq);

png